Consider a long cable or telephone wire (Fig. 315) that is imperfectly insulated, so that leaks occur along the entire length of the cable. The source S of the current i(x, t) in the cable is at x = 0, the receiving end T at x = l. The current flows from S to T and through the load, and returns to the ground. Let the constants R, L, C, and G denote the resistance, inductance, capacitance to ground, and conductance to ground, respectively, of the cable per unit length.

(a) Show that (€œfirst transmission line equation€)

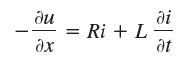
where u (x, t) is the potential in the cable. Apply Kirchhoff€™s voltage law to a small portion of the cable between x and x+ Δx (difference of the potentials at x and x + Δx = resistive drop + inductive drop).

(b) Show that elimination of i or u from the transmission line equations leads to

(c) For a submarine cable, G is negligible and the frequencies are low. Show that this leads to the so-called submarine cable equations or telegraph equations

Find the potential in a submarine cable with ends (x = 0, x = l) grounded and initial voltage distribution U₀ = const.

(d) Show that in the case of alternating currents of high frequencies the equations in (c) can be approximated by the so-called high-frequency line equations

Solve the first of them, assuming that the initial potential is

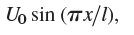
and u_t (x, 0) = 0 and u = 0 at the ends x = 0 and x = l for all t.

Load ai = Ri + L- at