Find the temperature w(x, t) in a semi-infinite laterally insulated bar extending from x = 0 along the x-axis to infinity, assuming that the initial temperature is 0, w(x, t) → 0 as x → ∞ for every fixed t ≥ 0, and w(0, t) = f(t). Proceed as follows.

Let w (0, t) = f(t) = u(t). Denote the corresponding w, W, and F by w₀, W₀, and F₀. Show that then in Prob. 10,

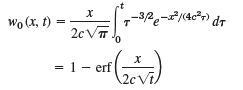
with the error function erf.

Data from Prob. 10

Find the temperature w(x, t) in a semi-infinite laterally insulated bar extending from x = 0 along the x-axis to infinity, assuming that the initial temperature is 0, w(x, t) → 0 as x → ∞ for every fixed t ≥ 0, and w(0, t) = f(t). Proceed as follows.

Applying the convolution theorem, show that in Prob. 9,

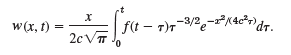
Data from Prob. 9

Find the temperature w(x, t) in a semi-infinite laterally insulated bar extending from x = 0 along the x-axis to infinity, assuming that the initial temperature is 0, w(x, t) → 0 as x → ∞ for every fixed t ≥ 0, and w(0, t) = f(t). Proceed as follows.

Set up the model and show that the Laplace transform leads to

and

Transcribed Image Text:

Wo (x, t) = X = 7-3/2e-/(4c7) dT 2cV X 2cVt = 1 erf|