(a) Prove that if (psi(x)) is a solution of the Dirac equation, Eq. (4.4.59), then it is...
Question:
(a) Prove that if \(\psi(x)\) is a solution of the Dirac equation, Eq. (4.4.59), then it is also a solution of the Klein-Gordon equation, Eq. (4.3.12).
(b) Prove that \(\partial_{\mu}\) and \(\partial_{u}\) commute, whereas \(D_{\mu}\) and \(D_{u}\) do not. Evaluate \(\left[D_{\mu}, D_{u}\right] \psi=\) \(D_{\mu}\left(D_{u} \psi\right)-D_{u}\left(D_{\mu} \psi\right)\) and so prove 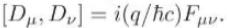
(c) Prove that if \(\psi(x)\) is a solution of the Dirac equation in the presence of an electromagnetic field, Eq. (4.4.61), it is also a solution of a modified Klein-Gordon equation,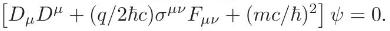
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Introduction To Quantum Field Theory Classical Mechanics To Gauge Field Theories
ISBN: 9781108470902
1st Edition
Authors: Anthony G. Williams
Question Posted:





