Prove the general thermodynamic relationship [left(frac{partial c_{p}}{partial p} ight)_{T}=-Tleft(frac{partial^{2} v}{partial T^{2}} ight)_{p}] and evaluate an expression for

Prove the general thermodynamic relationship

\[\left(\frac{\partial c_{p}}{\partial p}\right)_{T}=-T\left(\frac{\partial^{2} v}{\partial T^{2}}\right)_{p}\]

and evaluate an expression for the variation of \(c_{p}\) with pressure for a van der Waals gas which obeys a law

\[p=\frac{\Re T}{v_{m}-\mathrm{b}}-\frac{\mathrm{a}}{v_{m}^{2}}\]

where the suffix, \(m\), indicates molar quantities and \(\Re\) is the Universal gas constant.

It is possible to represent the properties of water by such an equation, where

\[\mathrm{a}=5.525 \frac{\left(\mathrm{m}^{3}\right)^{2} \mathrm{bar}}{(\mathrm{kmol})^{2}} ; \quad \mathrm{b}=0.03042 \frac{\mathrm{m}^{3}}{\mathrm{kmol}} ; \Re=8.3143 \mathrm{~kJ} / \mathrm{kmol} \mathrm{K} .\]

Evaluate the change in \(c_{p}\) as the pressure of superheated water vapour is increased from 175 bar to 200 bar at a constant temperature of \(425^{\circ} \mathrm{C}\). Compare this with the value you would expect from the steam tables abstracted below.

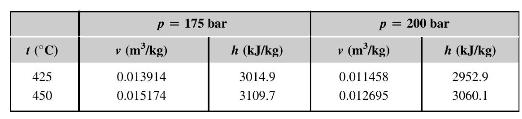
What is the value of \(\left(\frac{\partial c_{p}}{\partial p}\right)_{T}\) of a gas which obeys the Clausius equation of state, \(p=\frac{\Re T}{v_{m}-\mathrm{b}}\) ?

Transcribed Image Text:

p = 175 bar p = 200 bar 1 (C) v (m/kg) h (kJ/kg) v (m/kg) h (kJ/kg) 425 0.013914 3014.9 0.011458 2952.9 450 0.015174 3109.7 0.012695 3060.1