Show that, for a pure substance, [left(frac{partial s}{partial T} ight)_{p}=left(frac{partial s}{partial T} ight)_{v}+left(frac{partial s}{partial v} ight)_{T}left(frac{partial v}{partial

Question:

Show that, for a pure substance,

\[\left(\frac{\partial s}{\partial T}\right)_{p}=\left(\frac{\partial s}{\partial T}\right)_{v}+\left(\frac{\partial s}{\partial v}\right)_{T}\left(\frac{\partial v}{\partial T}\right)_{p}\]

and from this, prove that

\[c_{p}-c_{v}=T\left(\frac{\partial p}{\partial T}\right)_{v}\left(\frac{\partial v}{\partial T}\right)_{p} .\]

The following table gives values of the specific volume of water, in cubic metres per kilogram. A quantity of water is initially at \(30^{\circ} \mathrm{C}, 20 \mathrm{bar}\) and occupies a volume of \(0.2 \mathrm{~m}^{3}\). It is heated at constant volume to \(50{ }^{\circ} \mathrm{C}\) and then cooled at constant pressure to \(30^{\circ} \mathrm{C}\). Calculate the net heat transfer to the water.

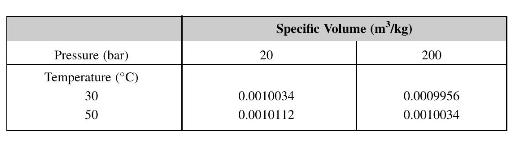
image text in transcribed