Use Eq. (6.2.129) and symmetry to explain why \(\hat{\mathbf{P}}\) and \(\hat{M}^{i j}\) do not need normal-ordering. Show that for a scalar boson field

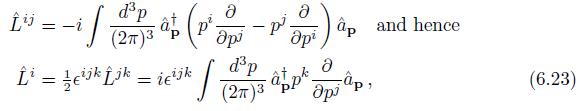
where \(\hat{L}^{\mu u}\) is the coordinate component of \(\hat{M}^{\mu u}\) and \(\hat{\mathbf{L}}\) is the orbital angular momentum operator. Show that the orbital angular momentum of a single boson at rest is zero, i.e., \(\hat{\mathbf{L}}|\mathbf{p}=\mathbf{0}angle=0\).

Transcribed Image Text:

Lij =-i -is. = dp (2) p - a p. ap and hence dp == t, (2)3 ap: (6.23)