A commutative diagram 

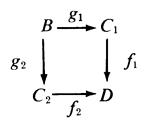
of morphisms of a category e is called a pullback for ∫₁ and ∫₂ if for every pair of morphisms h₁ : B'-----+ C₁, h₂: B' → C₂ such that ∫₁h₁ = ∫₂h₂ there exists a unique morphism t: B' → B such that h₁ = g₁t and h₂ = g₂t.

(a) If there is another pullback diagram for ∫₁∫₂ with B₁ in the upper left-hand corner, then B and B₁ are equivalent.

(b) In the pullback diagram above, if ∫₂ is a monomorphism, then so is g₁.

(c) Every pair of functions ∫₁ :C₁ → D,∫₂ : C₂ → D in the category of sets has a pullback. 

Transcribed Image Text:

82 B₁C₁ Į fi C₂ D