(a) Let S be a nonempty set and let N^s be the set of all functions φ : S → N such that φ(s) ≠ O for at most a finite number of elements s ϵ S. Then N^s is a multiplicative abelian monoid with product defined by 

The identity element in N^s is the zero function.

(b) For each x ϵ S and i ϵ N let xⁱ ϵ N^s be defined by xⁱ{x) = i and xⁱ(s) ≠ 0 for s ≠ x. If φ ϵ N^s and x₁, ... , X_n are the only elements of S such that φ(x_i) ≠ 0, then in N^s, φ = x₁ⁱ¹x₂ⁱ². · ·X_nⁱⁿ, where i₁ = φ(x_i).

(c) If R is a ring with identity let R[S] be the set of all functions ∫: N^s → R such that ∫(φ) ≠ O for at most a finite number of φ ϵ N^s. Then R[S] is a ring with identity, where addition and multiplication are defined as follows: 

where the sum is over all pairs (θ,ζ) such that θζ = φ. R[S] is called the ring of polynomials in S over R.

(d) For each φ = x₁ⁱ¹ • • • X_nⁱⁿ ϵ N^s and each r ϵ R we denote by rx₁ⁱ¹ • • • X_nⁱⁿ the function N^s → R which is r at φ and O elsewhere. Then every nonzero element ∫ of R[S] can be written in the form 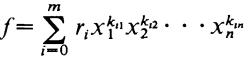with the r_i ϵ R, X_i ϵ S and k_ij ϵ N all uniquely determined.

(e) If S is finite of cardinality n, then R[S] ≅ R[x₁, .•. , x_n]- 

Transcribed Image Text:

(c)(s) = (s) + (s) (4,4 € NS;s & S).