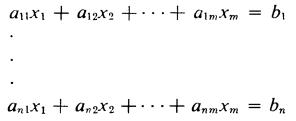(a) The system of n linear equations in m unknowns x, over a field K has a (simultaneous) solution if and only if the matrix equation AX = B has a solution X, where A is the n X m matrix (a_ij), X is the m X₁ column vector (x₁, x₂ • • •xm)^t and Bis then x₁ column vector (b₁b₂ • • -b_n)^t

(b) If A₁,B₁ are matrices obtained from A,B respectively by performing the same sequence of elementary row operations on both A₁ and B₁ then X is a solution of AX = B if and only if X is a solution of A₁X = B₁.

(c) Let C be the n X (m + 1) matrix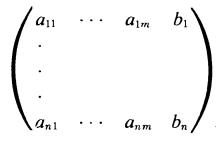 

Then AX = B has solution if and only if rank A = rank C. In this case the solution is unique if and only if rank A = m.

(d) The system AX = B is homogeneous if B is the zero column vector. A homogeneous system AX = B has a nontrivial solution (that is, not all x_i = 0) if and only if rank A < m (in particular, if n < m). 

Transcribed Image Text:

anxi + a₁2x₂ + ... + aim xm b₁ anix₁ + a2x₂ + ... + anmxm = bn