There are only two distinct groups of order 4. One of them is the group for rotations
Question:
There are only two distinct groups of order 4. One of them is the group for rotations of a square, Problem 8 . Here is the product table of the other.
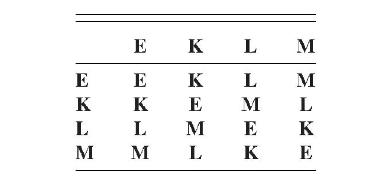
Show that \(\{\mathbf{E}, \mathbf{K}, \mathbf{L}, \mathbf{M}\}\) indeed form a group. Is it an Abelian group? Is it a cyclic group? Explain.
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

An Introduction To Groups And Their Matrices For Science Students
ISBN: 9781108831086
1st Edition
Authors: Robert Kolenkow
Question Posted: