A liquid-phase biological reaction is used to produce an intermediate chemical for use in the pharmaceutical industry. The reaction occurs in a large, well-stirred bioreactor that is illustrated in Figure P14.8. Because this chemical is temperature sensitive, the maximum operating temperature in the reactor is limited to 65°C. The feed material is fed to the reactor through a heat exchanger that can increase the temperature of the reactants (contents of the reactor), which in turn increases the rate of the reaction. This is illustrated in Figure P14.8. The time spent in the bioreactor (space time) must be adjusted in order to obtain the desired conversion of reactant. As the temperature in the reactor increases, so does the reaction rate, and hence the size (and cost) of the reactor required to give the desired conversion decreases. It is desired to determine the optimal temperature at which to maintain the reactor (and to preheat the feed). The costs to be considered are the purchase cost of the reactor and heat exchanger and the operating cost for the energy to heat the feed.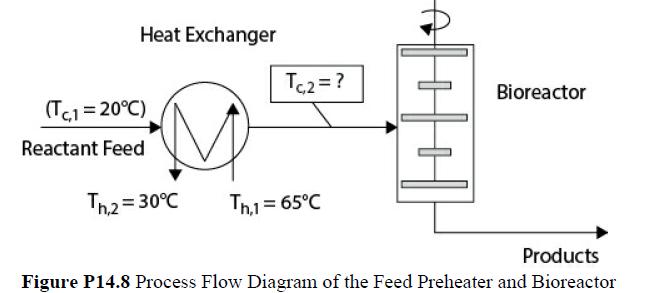

It is desired to optimize the preheat temperature for a flow of 5000 gal/h. The feed has the properties of water (ρ = 1000 kg/m³, C_p = 4.18 kJ/kg°C) and enters the heat exchanger at a temperature of 20°C. Reactor feed is to be heated with a heating medium that is available at a temperature of 65°C and must leave the heat exchanger at 30°C. Therefore, the desired reactor inlet temperature is adjusted by changing the flowrate of the heating medium. The physical properties of the heating medium are ρ = 920 kg/m³, and C_p = 2.2 kJ/kg°C.

The reaction rate for this reaction, −r_A, is given in terms of the concentration of reactant A (C_A) by the following equation:

The design equation for the reactor is given by

where V is the reactor volume (m³), v_o is the volumetric flowrate of fluid into the reactor (m³/s), and X_A is the conversion (assumed to be 80%, or 0.8, for this reaction).

The design equation for the heat exchanger is given by

The optimal reactor inlet temperature is the one that minimizes the equivalent annual operating costs (EAOC) given by

where PC_i is the purchase equipment cost for the heat exchanger and reactor and UC is the operating (utility) cost for the heating medium. For this problem use i = 7% p.a. and n = 12 years.

The purchase cost of the reactor is given by

where V is the volume of the reactor in m³. The cost of the heat exchanger is

where A is the area of the heat exchanger in m³. The cost of the heating medium is

Present your final results as two plots. The first should show how each term in Equation (P14.8.6) changes with T_C,2,and the second plot should show the EAOC (y-axis) as a function of T_C,2,(x-axis). Explain the reason for the trends seen in each of these plots.

Transcribed Image Text:

Heat Exchanger (TC,1 = 20°C) Reactant Feed Th,2 = 30°C Tc2= ? Th,1 = 65°C C Bioreactor Products Figure P14.8 Process Flow Diagram of the Feed Preheater and Bioreactor