Consider the determination of the optimal cycle time for a batch reactor similar to that covered in Example 14.7. Repeat the analysis using the following parameters: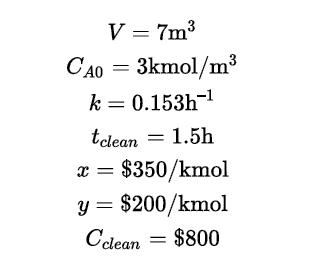

Example 14.7

When pumping a liquid from one location to another, the diameter of the pipeline plays a critical role in determining the amount of power (electricity) required to pump the liquid. For a given flow of liquid, the amount of power required by the pump to move the liquid between locations decreases as the diameter of the pipe increases. However, the cost of the piping increases with diameter. Therefore, for a given flowrate of liquid and a given distance between locations, there exists an optimal pipe diameter that minimizes the cost of the system comprising the pump and pipe.

It is required to find the optimal pipe diameter for a system through which 100,000 barrels per day of oil are pumped over a distance of 100 miles.

The overall cost of the system includes the equipment costs (pump and piping), which are one-time purchases, and the operating cost (electricity for the pump), which occurs all the time. The time value of money must be taken into consideration when defining an objective function. For this project, it is desired to minimize the equivalent annual operating cost (EAOC) of the pump and piping system that is defined in Equation (P14.7.1):

where PC is the purchase cost of the pump and the pipe, and UC is the operating (utility) cost for the utilities (electricity to run the pump). Assume that the effective interest rate is 9% p.a. and that the length of the project, n, is 15 years.

The relationships between the flowrate (Q) of oil, the pipe diameter (d ), and the power required for the pump 

are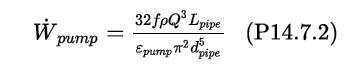

where ρ is the density of the fluid being pumped (930 kg/m3), and ε_pump is the efficiency of the pump (assume this is 85%, or 0.85). Using SI units (m, s, kg), the units of power in Equation (P14.7.2) are Watts (W). Assume that the cost of electricity is $0.05/kWh, where a kWh is the energy used in one hour by a device consuming 1 kW. Assume that the pump operates 24 h per day 365 days per year.

In Equation (P14.7.2), the term f is the friction factor, which is a function of the flowrate and the pipe diameter and is given by Equation (P14.7.3):

where ε is the roughness of the pipe (assume a value of 0.045 mm),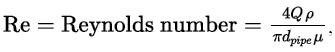

and μ is the viscosity of the oil (assume μ = 0.01 kg/m/s).

The cost of the pump can be estimated using Equation (P14.7.4):

The cost of piping is given by Equation (P14.7.5):

Present your final results as two plots. The first should show how each term in Equation (P14.7.1) changes with d_pipe (x-axis), and the second plot should show the EAOC (y-axis) as a function of d_pipe (x-axis). Explain the reason for the trends seen in each of these plots.

Transcribed Image Text:

V = 7m³ CA0 = 3kmol/m³ k = 0.153h-¹ tclean = 1.5h x = $350/kmol y = $200/kmol Cclean = $800