Prove that if v is an eigenvector of A with eigenvalue and w is an eigenvector of A T with a different eigenvalue , then v and w are orthogonal vectors with respect to the dot product Illustrate this result when (i) (ii) A (2 1 3

Question: Prove that if v is an eigenvector of A with eigenvalue and w is an eigenvector of A T with a different eigenvalue

Prove that if v is an eigenvector of A with eigenvalue λ and w is an eigenvector of A^Twith a different eigenvalue μ ≠ λ, then v and w are orthogonal vectors with respect to the dot product. Illustrate this result when

(i)

A = (2 -1 3

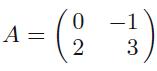
(ii)

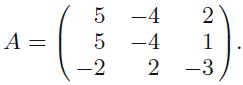
A = (2 -1 3

Step by Step Solution

★★★★★

3.34 Rating (157 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

ANSWER Proof Let v be an eigenvector of A with eigenvalue and w be an eigenvector of AT with eigenva... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Applied Linear Algebra Questions!

(a) Prove that every eigenvalue of a matrix A is also an eigenvalue of its transpose AT. (b) Do they have the same eigenvectors? Prove that if v is an eigenvector of A with eigenvalue and w is an...

If v is an eigenvector of A with corresponding eigenvalue and c is a scalar, show that v is an eigenvector of A - cI with corresponding eigenvalue - c.

Surfs Up Corporation is having financial difficulty and therefore has asked Gotham National Bank to restructure its $5,000,000 note outstanding. The note has 3 years remaining and pays a current rate...

1. (2 pt) Here is an identity for the exponential function er. in n ! We can define the exponential of a matrix in a similar fashion: exp (A) :- An n ! Suppose that A had eigenvector V with...

Hi, I need help with linear algebra question. Thanks. Problem 3. The Matrix Exponential: Algebraic Properties Recall that for a scalar a E R, we can write its exponential e" as a Taylor series that...

Question 6: For an invertible matrix A, prove that A and AI have the same eigenvectors. How are the eigenvalues of A related to the eigenvalues of A -1? Letting x be an eigenvector of A gives Ax = 1x...

Let V be a finite-dimensional complex inner product vector space, and let T be a normal linear operator on V. Prove that v E V is an eigenvector of T with eigenvalue dEC if and only if v is an...

6. Use Gaussian elimination to find the determinant of the matrix 1 3 2 4 1648 A = 1300 2 64 12, 7. Find the determinant of the linear transformation T(S)=2f+3f' from P to P. Recall that P (a+b+cr:...

1 Is v= an eigenvector of A = -9 5 -2 -2 ? If so, find the eigenvalue. Select the correct choice below and, if necessary, fill in the answer box within your choice. A. Yes, v is an eigenvector of A....

5 2 Consider the matrix A = (-2 1 (a) Find the eigenvalues of A. Show that A has only one linearly independent eigenvector. (b) Suppose A is the eigenvalue, and v is the eigenvector in (a). Find a...

Harry drove for 3 hours on the freeway, then decreased his speed by 20 miles per hour and drove for 5 more hours on a country road. If his total trip was 436 miles, then what was his speed on the...

Analyse the company's financial performance. Calculate the following financial ratios: 1. Profitability ratios 2. Liquidity ratios 3. Leverage ratios 4. Asset management ratios 5. Market value ratio...

Which is an explicit requirement in the cellular to tooth fairy rule on solicitation with respect to published fee information the practitioner to retain copies of all fee schedules for at least 3 6...

Explain the advantages and disadvan- tages of a limited partnership.

Answer Exercise 5.7.10 when f(x) = (a) x (b) x2(2Ï - x)2 (c) sin x , 0

Let f(x) = x(2 - x) be sampled on n = 128 equally spaced points between 0 and 2 . Use a random number generator with - 1

The signal in Figure 5.15 was obtained from the explicit formula Noise was added by using a random number generator. Experiment with different intensities of noise and different numbers of sample...

Stuart Corporation paid one of its sales representatives $10,000 during the month of March. The rep is paid a base salary plus $14 per unit of product sold. During March, the rep sold 120 units....

Charging a rate of interest higher than that allowed by law is usury. True False

What are some steps taken by both the FASB and IASB to move to fair value measurement for financial instruments? In what ways have some of the approaches differed