Under the set up of Theorem 8 42, explain why Theorem 8 42 immediately implies that q j is a unit eigenvector of K associated with its j th largest eigenvalue j 2 j , which therefore is, up to a factor, the j th principal variance Summarizing, we have proved the Fundamental Theorem of Principal Component Analysis A max vT Kv v 2 v 0, vV1 V V j 1 0

Question: Under the set-up of Theorem 8.42, explain why Theorem 8.42 immediately implies that q j is a unit eigenvector of K associated with its j

Under the set-up of Theorem 8.42, explain why

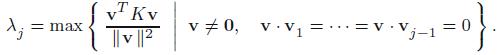
A; = max vT Kv || v ||2 { v = 0,

Theorem 8.42 immediately implies that q_jis a unit eigenvector of K associated with its j^th largest eigenvalue λ_j = σ²_j, which therefore is, up to a factor, the j^th principal variance. Summarizing, we have proved the Fundamental Theorem of Principal Component Analysis.

A; = max vT Kv || v ||2 { v = 0, vV1 = = V. V j - 1 - 0

Step by Step Solution

★★★★★

3.38 Rating (170 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Theorem 842 provides the Singular Value Decomposition SVD of a data matrix X where X is an n p matri... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Applied Linear Algebra Questions!

Managing Scope Changes Case Study Scope changes on a project can occur regardless of how well the project is planned or executed. Scope changes can be the result of something that was omitted during...

Write a literature review for your study. See below for an example of a literature review. Your literature review should provide both analysis and synthesis of previous studies as related to the...

Read the case study "Southwest Airlines," found in Part 2 of your textbook. Review the "Guide to Case Analysis" found on pp. CA1 - CA11 of your textbook. (This guide follows the last case in the...

Briefly describe ASCII and Unicode and draw attention to any relationship between them. [3 marks] (b) Briefly explain what a Reader is in the context of reading characters from data. [3 marks] A...

Under the set-up of Theorem 8.30, explain why j max V.VI = . . .

Under the setup of Theorem 3.2.1, show there always exists MP tests that are nested in the sense of Problem 3.17(iii).

Under the setup of Theorem 3.2.1, show that there always exist MP tests that are nested in the sense of Problem 3.17(iii).

Chapter 5 Discrete Markov process Suppose we have a sequence of random variables, {X0 , X1 , . . .} = {Xn } , which is also n=0 called a stochastic process. In this chapter, we study a commonly used...

1. Look at the following binomial graphs: risky project, the risky debt contract, and the equity security. Which of those graphs is equivalent to a call option with strike price X? 2. Copy the risky...

needanswersof parta, b, c, d, e, f.thanks a. The main goal is to show that if u = (U1, 2) and v = (v1, v2) are vectors in R?, then, and 7 are parallel to each other if and only if u1V2 - 2V1 = 0....

Consider the production function presented in the table below: a. If the firm decides to employ 6 units of capital and 1 worker, what is its output? b. What other combinations of capital and labor...

Why does a shirt or blouse taken from a clothes dryer sometimes cling to your body?

Please write for me a term paper on Managerial accounting Topic : Capital budgeting

Limited partnerships offer limited liabil- ity for all partners. a. True b. False

Is Theorem 5.54 true as stated for complex matrices? If not, can you formulate a similar theorem that is true? What is the Fredholm alternative for complex matrices?

Decompose each of the following vectors with respect to the indicated subspace as v = w + z, where w W, z W¥. , W = span (b) 2 , W = span V 12 1 W= ker (-2-1 0 0 3 W = ker

Redo Exercise 5.6.1 using the weighted inner product (v, w) = v1w1 + 2v2w2 + 3v3w3 instead of the dot product.

How long will it take me if I invest 500 per month towards accumulating 50,000 and my investments will earn 0.50% per month.

Dennisport Corporation has an acid-test ratio of 2.3. It has current liabilities of $46,000 and noncurrent assets of $76,000. The corporation's current assets consist of cash, marketable securities,...

All Frute Company bottles and distributes Frute Ade, a fruit drink. The beverage is sold for 50 cents per 16-ounce bottle to retailers, who charge customers 70 cents per bottle. For the year 2017,...