A system of two homogeneous linear ordinary differential equations with constant coefficients can be written as

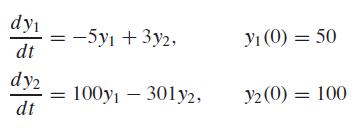
If you have taken a course in differential equations, you know that the solutions for such equations have the form y_i = ce^λt where c and are constants to be determined. Substituting this solution and its derivative into the original equations converts the system into an eigenvalue problem. The resulting eigenvalues and eigenvectors can then be used to derive the general solution to the differential equations. For example, for the two-equation case, the general solution can be written in terms of vectors as

where {ν_i} = the eigenvector corresponding to the i^th eigenvalue (λ_i) and the c’s are unknown coefficients that can be determined with the initial conditions.
(a) Convert the system into an eigenvalue problem.
(b) Use MATLAB to solve for the eigenvalues and eigenvectors.
(c) Employ the results of (b) and the initial conditions to determine the general solution.
(d) Develop a MATLAB plot of the solution for t = 0 to 1.

dyi dt dy2 dt = -5y1 + 3y2, 100y1 - 301y2, y (0) = 50 32 (0) = 100