The curvature of a slender column subject to an axial load P (Fig. P13.10) can be modeled

Question:

The curvature of a slender column subject to an axial load P (Fig. P13.10) can be modeled by

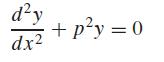
where

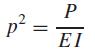
where E = the modulus of elasticity, and I = the moment of inertia of the cross section about its neutral axis. This model can be converted into an eigenvalue problem by substituting a centered finite-difference approximation for the second derivative to give

where i = a node located at a position along the rod’s interior, and x = the spacing between nodes. This equation can be expressed as

Writing this equation for a series of interior nodes along the axis of the column yields a homogeneous system of equations. For example, if the column is divided into five segments (i.e., four interior nodes), the result is An axially loaded wooden column has the following characteristics:
E = 10 ×10⁹Pa, I = 1.25 ×10^–5 m⁴, and L = 3 m.
For the five-segment, four-node representation:
(a) Implement the polynomial method with MATLAB to determine the eigenvalues for this system.
(b) Use the MATLAB eig function to determine the eigenvalues and eigenvectors.
(c) Use the power method to determine the largest eigenvalue and its corresponding eigenvector.