Use ode45 to integrate the differential equations for the system described in Prob. 23.19. Generate vertically stacked subplots of displacements (top) and velocities (bottom). Employ the fft function to compute the discrete Fourier transform (DFT) of the first mass’s displacement. Generate and plot a power spectrum in order to identify the system’s resonant frequencies.

Data From Problem 23.19

Two masses are attached to a wall by linear springs (Fig. P23.19). Force balances based on Newton’s second law  can be written as

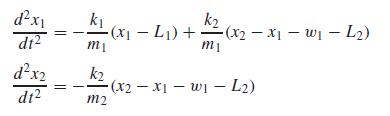
where k = the spring constants, m = mass, L = the length of the unstretched spring, and w = the width of the mass. Compute the positions of the masses as a function of time using the following parameter values: k₁ = k₂ = 5, m₁ = m₂ = 2, w1 = w₂ = 5, and L₁ = L₂ = 2. Set the initial conditions as x₁ = L₁ and x₂ = L₁ + w₁ + L₂ + 6. Perform the simulation from t = 0 to 20. Construct time-series plots of both the displacements and the velocities. In addition, produce a phaseplane plot of x₁ versus x₂.

dx d1 dx2 d1 mi k (x - L) + m2 m (xx wL2) (27-Im- 1x - 7x). -