Determine the probability mass function of \(X\) from the following cumulative distribution function:

\[ F(x)=\left\{\begin{array}{lr} 0 & x. \]

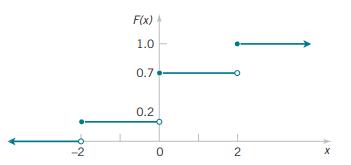
Figure 3.3 displays a plot of \(F(x)\). From the plot, the only points that receive nonzero probability are \(-2,0\), and 2 . The probability mass function at each point is the jump in the cumulative distribution function at the point. Therefore,

\[ \begin{aligned} & f(-2)=0.2-0=0.2 \\ & f(0)=0.7-0.2=0.5 \\ & f(2)=1.0-0.7=0.3 \end{aligned} \]

Figure 3.3

-2 F(x)+ 1.0 0.7 0.2 0 2 x