To test for equality of variances in \(k\) blocks of sizes \(n_{1}, \ldots, n_{k}\), the REML procedure goes as follows. First, \(\mathrm{bl} k\) is the \(k\)-dimensional subspace of \(\mathbb{R}^{n}\) spanned by the block indicators \(b_{1}, \ldots, b_{k}\). Second, \(I_{r}\) is the restriction of the identity matrix to block \(r\), i.e., \(I_{r}(i, j)=\delta_{i j} b_{r}(i)\). The likelihood-ratio statistic is computed by fitting null and alternative models as follows: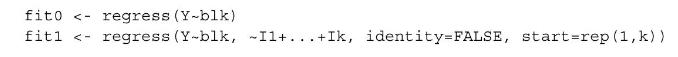

Show that the REML likelihood-ratio statistic \(2 f i t 1 \$ l l i k-2 f i t 0 \$ l l i k\) is equal to the gamma deviance statistic
\[
(n .-k) \log \left(s_{\text {pool }}^{2}ight)-\sum\left(n_{r}-1ight) \log \left(s_{r}^{2}ight),
\]
where \(s_{r}^{2}\) is the sample variance in block \(r\), and \(s_{\text {pool }}^{2}\) is the pooled variance. Bartlett's (1937) test for equality of variances is the REML statistic divided by the Bartlett correction factor

\[
1+\frac{1}{3(k-1)}\left(\sum_{r=1}^{k} \frac{1}{n_{r}-1}-\frac{1}{n-k}ight)
\]
What is the null distribution of the ratio?

Transcribed Image Text:

fit0 < regress (Y-blk) fit1 < regress (Y-blk, -I1+...+Ik, identity=FALSE, start=rep (1,k))