This exercise extends the hypergeometric distribution to multiple variables Consider a population with N items of k different types Assume that there are N 1 items of type 1, N 2 items of type 2, brvbar , N k items of type k so that N 1 N 2 brvbar brvbar N k N Suppose that a random sample of size n...

The probability function for X is The number of ways to ...

This exercise extends the hypergeometric distribution to multiple variables. Consider a population with N items of k

Question:

This exercise extends the hypergeometric to multiple variables. Consider a population with N items of k different types. Assume that there are N₁items of type 1, N₂items of type 2,€¦, N_kitems of type k so that N₁+ N₂+ €¦ + €¦ N_k= N. Suppose that a random sample of size n is selected, without replacement, from the population. Let X₁, X₂,€¦, X_kdenote the number of items of each type in the sample so that X₁+ X₂, + €¦ + €¦ + X_k= n. Show that for feasible values of n, x₁, x₂, €¦, x_k, N₁, N₂, €¦, N_k, the probability is

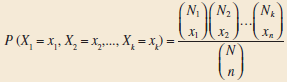
NE X1 P (X, = x,, X, = x,.., X, = x,) = C) X2 х,

Distribution
The word "distribution" has several meanings in the financial world, most of them pertaining to the payment of assets from a fund, account, or individual security to an investor or beneficiary. Retirement account distributions are among the most...

Fantastic news! We've Found the answer you've been seeking!