Suppose two friends live in different cities on a map, such as the Romania map shown in Figure 3.2. On every turn, we can simultaneously move each friend to a neighboring city on the map. The amount of time needed to move from city i to neighbor j is equal to the road distance d(i, j) between the cities, but on each turn the friend that arrives first must wait until the other one arrives (and calls the first on his/her cell phone) before the next turn can begin. We want the two friends to meet as quickly as possible.

a. Write a detailed formulation for this search problem. (You will find it helpful to define some formal notation here.)

b. Let D(i, j) be the straight-line distance between cities i and j. Which of the following heuristic functions are admissible? (i) D(i, j); (ii) 2 · D(i, j); (iii) D(i, j)/2.

c. Are there completely connected maps for which no solution exists?

d. Are there maps in which all solutions require one friend to visit the same city twice?

Figure 3.2

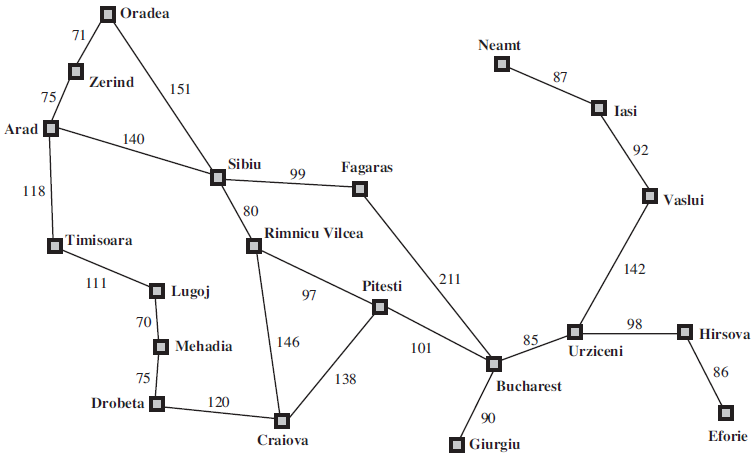
|Oradea 71 Neamt 87 Zerind 151 75 Iasi Arad I 140 92 Sibiu Fagaras 99 118 Vaslui 80 Rimnicu Vilcea |Timisoara 142 211 111 Pitesti Lugoj 97 70 98 Hirsova 85 146 Mehadia 101 Urziceni 86 75 138 Bucharest 120 Drobeta 90 Eforie Craiova |Giurgiu