The operation of arc reversal ARC REVERSAL in a Bayesian network allows us to change the direction of an arc X †’ Y while preserving the joint probability distribution that the network represents (Shachter, 1986). Arc reversal may require introducing new arcs: all the parents of X also become parents of Y, and all parents of Y also become parents of X.

a. Assume that X and Y start with m and n parents, respectively, and that all variables have k values. By calculating the change in size for the CPTs of X and Y, show that the total number of parameters in the network cannot decrease during arc reversal.

b. Under what circumstances can the total number remain constant?

c. Let the parents of X be U ˆª V and the parents of Y be V ˆª W, where U and W are disjoint. The formulas for the new CPTs after arc reversal are as follows:

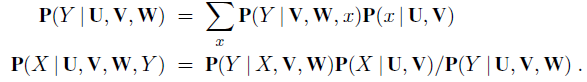
Prove that the new network expresses the same joint distribution over all variables as the original network.

Transcribed Image Text:

P(Y |U, V, W) > P(Y | V, W, x)P(x|U, V) P(X |U, V, W, Y) P(Y X, V, W)P(X |U, V)/P(Y |U, V, W) .