Add rules for (multiple) prepositional phrases to the English grammar of Example 3.3.6.

Data from Example 3.3.6

Our final example is not from the predicate calculus but consists of a set of rewrite rules for parsing sentences in a subset of English grammar. Rewrite rules take an expression and transform it into another by replacing the pattern on one side of the arrow (↔) with the pattern on the other side. For example, a set of rewrite rules could be defined to change an expression in one language, such as English, into another language (perhaps French or a predicate calculus clause). The rewrite rules given here transform a subset of English sentences into higher level grammatical constructs such as noun phrase, verb phrase, and sentence. These rules are used to parse sequences of words, i.e., to determine whether they are well-formed sentences (whether they are grammatically correct or not) and to model the linguistic structure of the sentences.

Five rules for a simple subset of English grammar are:

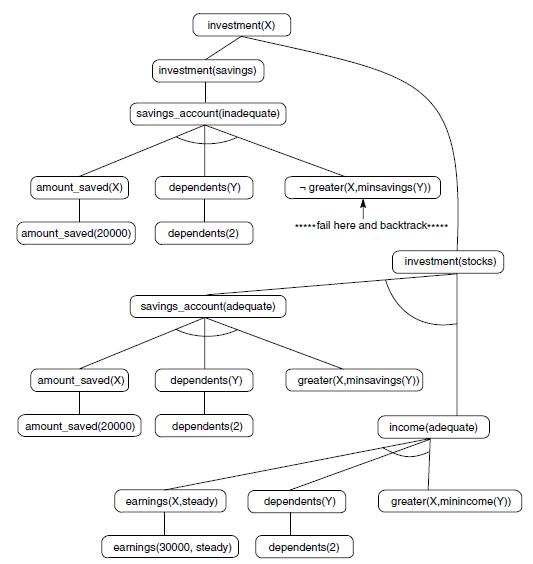
In addition to these grammar rules, a parser needs a dictionary of words in the language. These words are called the terminals of the grammar. They are  defined by their parts of speech using rewrite rules. In the following dictionary, “a,” “the,” “man,” “dog,”

“likes,” and “bites” are the terminals of our very simple grammar:

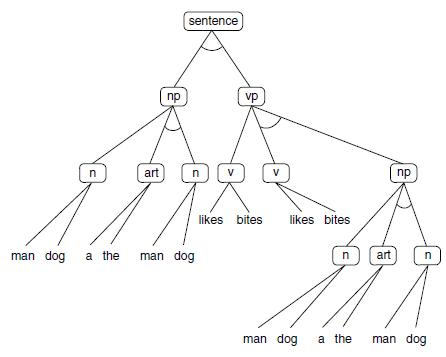
These rewrite rules define the and/or graph of Figure 3.27, where sentence is the root. The elements on the left of a rule correspond to and nodes in the graph. Multiple rules with the same conclusion form the or nodes. Notice that the leaf or terminal nodes of this graph are the English words in the grammar (hence, they are called terminals).

An expression is well formed in a grammar if it consists entirely of terminal symbols and there is a series of substitutions in the expression using rewrite rules that reduce it to the sentence symbol. Alternatively, this may be seen as constructing a parse tree that has the words of the expression as its leaves and the sentence symbol as its root.

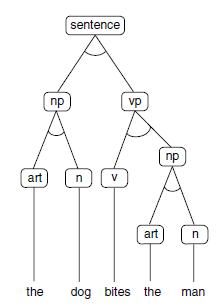
For example, we may parse the sentence the dog bites the man, constructing the parse tree of Figure 3.28. This tree is a subtree of the and/or graph of Figure 3.27 and is constructed by searching this graph. A data-driven parsing algorithm would implement this by matching right-hand sides of rewrite rules with patterns in the sentence, trying these matches in the order in which the rules are written. Once a match is found, the part of the expression matching the right-hand side of the rule is replaced by the pattern on the left-hand side. This continues until the sentence is reduced to the symbol sentence (indicating a successful parse) or no more rules can be applied (indicating failure). A trace of the parse of the dog bites the man:

1. The first rule that will match is 7, rewriting the as art. This yields: art dog bites the man.

2. The next iteration would find a match for 7, yielding art dog bites art man.

3. Rule 8 will fire, producing art dog bites art n.

4. Rule 3 will fire to yield art dog bites np.

5. Rule 9 produces art n bites np.

6. Rule 3 may be applied, giving np bites np.

7. Rule 11 yields np v np.

8. Rule 5 yields np vp.

9. Rule 1 reduces this to sentence, accepting the expression as correct. 

The above example implements a data-directed depth-first parse, as it always applies the highest-level rule to the expression; e.g., art n reduces to np before bites reduces to v. Parsing could also be done in a goal-directed fashion, taking sentence as the starting string and finding a series of replacements of patterns that match left-hand sides of rules leading to a series of terminals that match the target sentence.

Parsing is important, not only for natural language (Chapter 15) but also for constructing compilers and interpreters for computer languages (Aho and Ullman 1977). The literature is full of parsing algorithms for all classes of languages. For example, many goal-directed parsing algorithms look ahead in the input stream to determine which rule to apply next.

In this example we have taken a very simple approach of searching the and/or graph in an uninformed fashion. One thing that is interesting in this example is the implementation of the search. This approach of keeping a record of the current expression and trying to match the rules in order is an example of using a production system to implement search. This is a major topic of Chapter 6.

Rewrite rules are also used to generate legal sentences according to the specifications of the grammar. Sentences may be generated by a goal-driven search, beginning with sentence as the top-level goal and ending when no more rules can be applied. This produces a string of terminal symbols that is a legal sentence in the grammar. For example:

A sentence is a np followed by a vp (rule 1). np is replaced by n (rule 2), giving n vp. Man is the first n available (rule 8), giving man vp. Now np is satisfied and vp is attempted. Rule 3 replaces vp with v, man v. Rule 10 replaces v with likes. Man likes is found as the first acceptable sentence. If it is desired to create all acceptable sentences, this search may be systematically repeated until all possibilities are tried and the entire state space has been searched exhaustively. This generates sentences including a man likes, the man likes, and so on. There are about 80 correct sentences that are produced by an exhaustive search. These include such semantic anomalies as the man bites the dog. Parsing and generation can be used together in a variety of ways to handle different problems. For instance, if it is desired to find all sentences to complete the string “the man,” then the problem solver may be given an incomplete string the man... . It can work upward in a data-driven fashion to produce the goal of completing the sentence rule (rule 1), where np is replaced by the man, and then work in a goal-driven fashion to determine all possible vps that will complete the sentence. This would create sentences such as the man likes, the man bites the man, and so on. Again, this example deals only with syntactic correctness. The issue of semantics (whether the string has a mapping into some “world” with “truth”) is entirely different. Chapter 2 examined the issue of constructing a logic-based semantics for expressions; for verifing sentences in natural language, the issue is much more difficult and is discussed in Chapter 15. In the next chapter we discuss the use of heuristics to focus search on the “best” possible portion of the state space. Chapter 6 discusses the production system and other software “architectures” for controlling state-space search.

Transcribed Image Text:

1. sentence np vp (A sentence is a noun phrase followed by a verb phrase. 2. np n (A noun phrase is a noun.)