Trace the goal-driven good-dog problem of Example 3.3.4 in a data-driven fashion.

Data from Example 3.3.4

This example is taken from the predicate calculus and represents a goal-driven graph search where the goal to be proved true in this situation is a predicate calculus expression containing variables. The axioms are the logical descriptions of a relationship between a dog, Fred, and his master, Sam. We assume that a cold day is not a warm day, bypassing issues such as the complexity added by equivalent expressions for predicates, an issue discussed further in Chapters 7 and 14. The facts and rules of this example are given as English sentences followed by their predicate calculus equivalents:

1. Fred is a collie. collie(fred).

2. Sam is Fred’s master. master(fred,sam).

3. The day is Saturday. day(saturday).

4. It is cold on Saturday. ¬ (warm(saturday)).

5. Fred is trained. trained(fred).

6. Spaniels are good dogs and so are trained collies. ∀ X[spaniel(X) ∨ (collie(X) ∧ trained(X)) → gooddog(X)]

7. If a dog is a good dog and has a master then he will be with his master. ∀ (X, Y, Z) [gooddog(X) ∧ master (X, Y) ∧ location (Y, Z) → location (X, Z)]

8. If it is Saturday and warm, then Sam is at the park. (day(saturday) ∧ warm(saturday)) → location(sam,park).

9. If it is Saturday and not warm, then Sam is at the museum. (day(saturday) ∧ ¬ (warm(saturday))) → location(sam,museum).

The goal is the expression ∃ X location(fred,X), meaning “where is fred?” A backward search algorithm examines alternative means of establishing this goal: if fred is a good dog and fred has a master and fred’s master is at a location then fred is at that location also. The premises of this rule are then examined: what does it mean to be a gooddog, etc.? This process continues, constructing the and/or graph of Figure 3.25.

Let us examine this search in more detail, particularly because it is an example of goal-driven search using the predicate calculus and it illustrates the role of unification in the generation of the search space. The problem to be solved is “where is fred?” More formally, it may be seen as determining a substitution for the variable X, if such a substitution exists, under which location(fred,X) is a logical consequence of the initial assertions.

When it is desired to determine Fred’s location, clauses are examined that have location as their conclusion, the first being clause 7. This conclusion, location(X,Z), is then unified with location(fred, X) by the substitutions {fred/X, X/Z}. The premises of this rule, under the same substitution set, form the and descendants of the top goal:

gooddog(fred) ∧ master(fred,Y) ∧ location (Y, X).

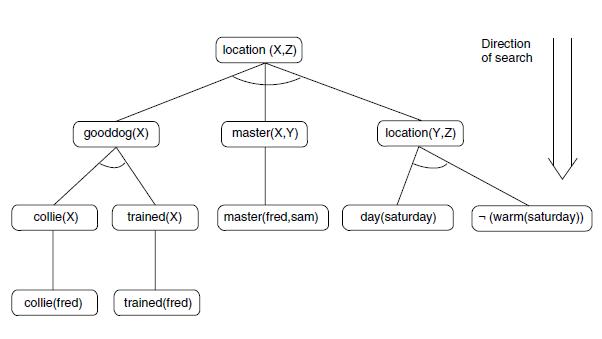
This expression may be interpreted as meaning that one way to find Fred is to see if Fred is a good dog, find out who Fred’s master is, and find out where the master is. The initial goal has thus been replaced by three subgoals. These are and nodes and all of them must be solved. To solve these subgoals, the problem solver first determines whether Fred is a gooddog. This matches the conclusion of clause 6 using the substitution {fred/X}. The premise of clause 6 is the or of two expressions:

spaniel(fred) ∨ (collie(fred) ∧ trained(fred))

The first of these or nodes is spaniel(fred). The database does not contain this assertion, so the problem solver must assume it is false. The other or node is (collie(fred) ∧ trained(fred)), i.e., is Fred a collie and is Fred trained. Both of these need to be true, which they are by clauses 1 and 5.

This proves that gooddog(fred) is true. The problem solver then examines the second of the premises of clause 7: master(X,Y). Under the substitution {fred/X}, master(X,Y) becomes master(fred,Y), which unifies with the fact (clause 2) of master(fred,sam). This produces the unifying substitution of {sam/Y}, which also gives the value of sam to the third subgoal of clause 7, creating the new goal location(sam,X).

In solving this, assuming the problem solver tries rules in order, the goal location(sam,X) will first unify with the conclusion of clause 7. Note that the same rule is being tried with different bindings for X. Recall (Chapter 2) that X is a “dummy” variable and could have any name (any string beginning with an uppercase letter). Because the extent of the meaning of any variable name is contained within the clause in which it  appears, the predicate calculus has no global variables. Another way of saying this is that values of variables are passed to other clauses as parameters and have no fixed (memory) locations. Thus, the multiple occurrences of X in different rules in this example indicate different formal parameters (Section 14.3). In attempting to solve the premises of rule 7 with these new bindings, the problem solver will fail because sam is not a gooddog. Here, the search will backtrack to the goal location(sam,X) and try the next match, the conclusion of rule 8. This will also fail, which will cause another backtrack and a unification with the conclusion of clause 9, at(sam,museum). Because the premises of clause 9 are supported in the set of assertions (clauses 3 and 4), it follows that the conclusion of 9 is true. This final unification goes all the way back up the tree to finally answer ∃ X location(fred,X) with location(fred, museum).

It is important to examine carefully the nature of the goal-driven search of a graph and compare it with the data-driven search of Example 3.3.2. Further discussion of this issue, including a more rigorous comparison of these two methods of searching a graph, continues in the next example, but is seen in full detail only in the discussion of production systems in Chapter 6 and in the application to expert systems in Part IV. Another point implicit in this example is that the order of clauses affects the order of search. In the example above, the multiple location clauses were tried in order, with backtracking search eliminating those that failed to be proved true.