In Example 5, change 8/15(180 < < 270) to 8/15(270 < < 360). Data

In Example 5, change 8/15(180° < α < 270°) to − 8/15(270° < α < 360°).

Data from Example 5

Given that tan α = 8/15 (180°< α <  270°), find cos(α/2).

Knowing that tan α = 8/15 for a third-quadrant angle, we determine from Fig. 20.20 that cos α= −15/17. This means

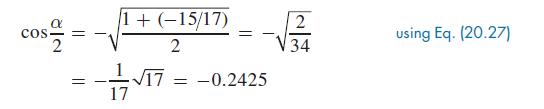
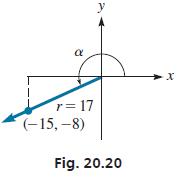
Because 180° < α < 270°, we know that 90° < α/2 < 135° 2 and therefore α/2 is in the second quadrant. Because the cosine is negative for second-quadrant angles, we use the negative value of the radical.

Transcribed Image Text:

cos2 = = 1 + (-15/17) 2 17 = 17 = -0.2425 2 34 using Eq. (20.27)