At the beginning of Section 4.5, we saw that under the alternative hypothesis that ~ N(,)

At the beginning of Section 4.5, we saw that under the alternative hypothesis that θ ~ N(θ,ψ) the predictive density for X̅ was N(θ₀, ψ + ϕ), so that

Show that a maximum of this density considered as a function of ψ occurs when ψ = (z² - 1)ϕ, which gives a possible value for ψ if z ≥ 1. Hence, show that if z ≥ 1 then for any such alternative hypothesis, the Bayes factor satisfies

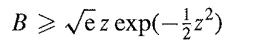
and deduce a bound for p₀ (depending on the value of π₀).

Transcribed Image Text:

P₁(x) = {2π(y +¢/n)}¯½ exp[-(x −00)²/(y + p/n)].