For the aspirin use data in Example 5.3, consider a scale mixing model as an alternative to

Question:

For the aspirin use data in Example 5.3, consider a scale mixing model as an alternative to normal random effects at the second stage. This is equivalent to a Student \(t\) second stage. Thus

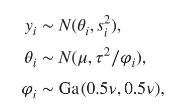
image text in transcribed

where \(v\) is an extra unknown degrees of freedom parameter. One possible prior is a uniform on \(1 / v\). How does this affect the posterior density for \(\mu\) as compared to a normal hierarchical model without scale mixing, and are any studies apparent as significant outliers (with 95\% intervals for \(\varphi_{i}\) entirely under 1).

Data from Example 5.3

image text in transcribed