In question 16 in Chapter 2, we supposed that the results of a certain test were known, on the basis of general theory, to be normally distributed about the same mean µ, with the same variance ∅, neither of which is known. In that question, we went on to suppose that your prior beliefs about (µ,∅) could be represented by a normal/chi-squared distribution with 

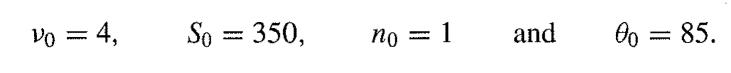
Find a semi-conjugate prior which has marginal distributions that are close to the marginal distributions of the normal/chi-squared prior but is such that the mean and variance are independent a priori. Now suppose as previously that 100 observations are obtained from the population with mean 89 and sample variance s² = 30. Find the posterior distribution of(µ,∅) Compare the posterior mean obtained by the EM algorithm with that obtained from the fully conjugate prior.

Question 16

Suppose that the results of a certain test are known, on the basis of general theory, to be normally distributed about the same mean μ with the same variance ∅, neither of which is known. Suppose further that your prior beliefs about (μ,∅) can be represented by a normal/chi-squared distribution with

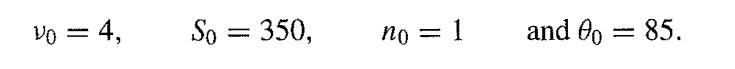
Now suppose that 100 observations are obtained from the population with mean 89 and sample variance s² = 30. Find the posterior distribution of (μ,ϕ). Compare 50% prior and posterior HDRs for μ.

Vo = 4, So = 350, no 1 1 and 00 = 85.