Modify the formula for the density of a one-to-one function g(x) of a random variable x to find an expression for the density of x² in terms of that of x, in both the continuous and discrete case. Hence, show that the square of a standard normal density has a chi-squared density on one degree of freedom as defined in Appendix A.

Appendix A.

Some facts are given about various common statistical distributions. In the case of continuous distributions, the (probability) density (function) p(x) equals the derivative of the (cumulative) distribution function F (x) = P(X ≤ x). In the case of discrete distributions, the (probability) density (function) p(x) equals the probability that the random variable X takes the value x. 

The mean or expectation is defined by 

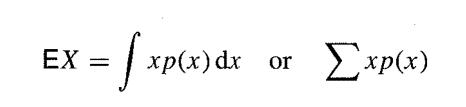
depending on whether the random variable is discrete or continuous. The variance is defined as 

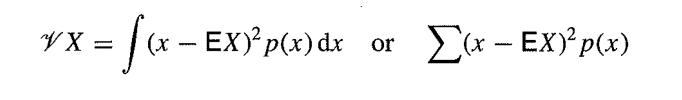
depending on whether the random variable is discrete or continuous. A mode is any value for which p(x) is a maximum; most common distributions have only one mode and so are called unimodal. A median is any value m such that both 

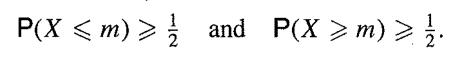
In the case of most continuous distributions, there is a unique median m and 

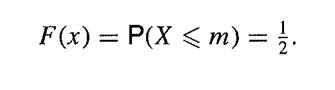
There is a well-known empirical relationship that 

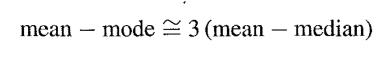
or equivalently

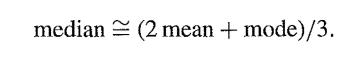
Some theoretical grounds for this relationship based on Gram-Charlier or Edgeworth expansions can be found in Lee (1991) or Kendall, Stewart and Ord (1987,. Section 2.11). 

Further material can be found in Rothschild and Logothetis (1986) or Evans, Hastings and Peacock (1993), with a more detailed account in Johnson et al. (2005), Johnson et al. (1994-1995), Balakrishnan et al. (2012) and Fang, Kotz and Wang (1989).

EX = xp(x) dx or = [xp(x) dx xp(x)