Observations x 1 , x 2 , ... , x n are independently distributed given parameters 1 , 2 , ... , n

Observations x₁, x₂, ... , x_n are independently distributed given parameters θ₁, θ₂, ... ,θ_n according to the Poisson distribution p(x_i ∣θ) = θ_i^xi exp(-0_i)/x_i. The prior distribution for θ is constructed hierarchically. First, the θ_is are assumed to be independently identically distributed given a hyperparameter ϕ according to the exponential distribution p(θ_i∣ϕ) = ϕ exp(-ϕθ_i) for θ_i ≥ 0 and then ϕ is given the improper uniform prior p (ϕ) ∝ 1 for ϕ ≥ 0. Provided that nX̅ > 1, prove that the posterior distribution of z = 1 / (1 + ϕ) has the beta form 

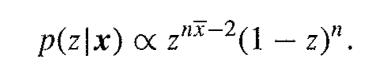
Thereby show that the posterior means of the θ_i are shrunk by a factor (nX̅ - 1)/(nX̅ + n) relative to the usual classical procedure which estimates each of the θ_i by X̅_i. 

What happens if nX̅ ≤ 1?

p(z|x) x zx-2(1-z)". z).