Suppose that a continuous random variable X has mean, and variance . By writing and using a lower bound for the integrand in the latter

Suppose that a continuous random variable X has meanµ, and variance ϕ. By writing 

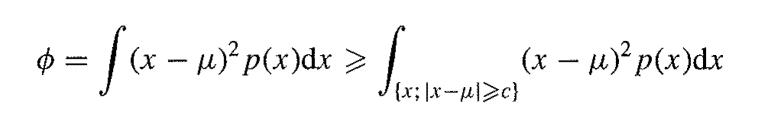
and using a lower bound for the integrand in the latter integral, prove that 

Show that the result also holds for discrete random variables. [This result is known as Cebysev's Inequality (the name is spelt in many other ways, including Chebyshev and Tchebycheff).]

= f(x )p(x)dx > Suite- (x )p(x)dx - {x;\x->c}