The Helmert transformation is defined by the matrix 

so that the element a_ij in row i, column j is

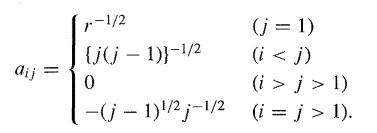
It is also useful to write a_j for the ( column) vector which consists of the jth column of the matrix A. Show that if the variates X_i are independently N(θ_i,1), then the variates W_j = a_j^T /(X - µ) = ∑_i a_{i j} (X_i - µ_j) are independently normally distributed with unit variance and such that EW_j = 0 for j > 1 and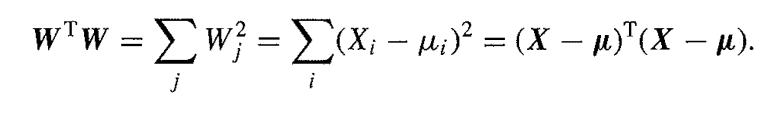  

By taking a_iJ ∝ θ_j - µ_j for i > j, a_jj = 0 for i jj such tha ∑_j a_ij = 0, extend this result to the general case and show that E W₁ ∝ y = ∑_i (0_i - µ_i)². Deduce that the distribution of a non-central chi-squared variate depends only of r and y.

Transcribed Image Text:

A = r-1/2 2-1/2 -1/2 -2-1/2 r-1/2 -1/2 r-1/2 ⠀ -1/2 0 0 0 : 0 6-1/2 6-1/2 -2 x 6-1/2 0 0 : 0 12-1/2 12-1/2 12-1/2 -3 x 12-1/2 0 ⠀ 0 ... ... ... ... ... {r(r-1)}-1/2 {r(r-1)}-¹/2 {r(r-1)}-1/2 {r(r-1)}-1/2 {r(r-1)}-1/2 ⠀ -(-1)¹/2-1/2