Exercise 12.11 Consider a Brownian motion {X(t)} with drift and diffusion coefficient . Suppose that X(0) = 0, and let denote the first

Exercise 12.11 Consider a Brownian motion {X(t)} with drift μ and diffusion coefficient σ. Suppose that X(0) = 0, and let τ denote the first time that the Brownian motion reaches the state x > 0. Prove that the density function for τ is given by

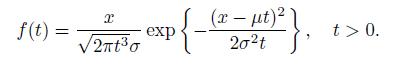
Note: For a standard Brownian motion {z(t)}, let τ be the first passage time to the boundary a(t) > 0. If the derivative a′(t) exists and is continuous, then the density function f(t) for τ satisfies the equation

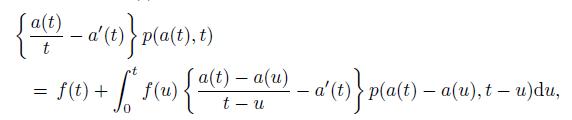
where p(x, t) is the transition density function of {z(t)}. See Williams (1992)
for details.

f(t) = x 2t (x-t) exp 202t }, t> 0.