Exercise 13.2 Suppose that a diffusion process {X(t)} with drift function (x) and diffusion function (x) has

Exercise 13.2 Suppose that a diffusion process {X(t)} with drift function

μ(x) and diffusion function σ(x) has absorbing boundaries a and

b, where a

b, and consider the first passage time Tz that the process reaches the boundary z, z =

a, b, for the first time.We are interested in the probability

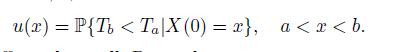
Let h > 0 be sufficiently small. Prove that

Also, assuming that u(x) is sufficiently smooth, prove that

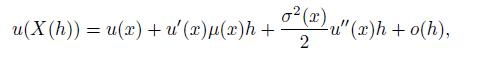
using Taylor’s expansion. Finally, prove that u(x) satisfies the ordinary differential equation (ODE)

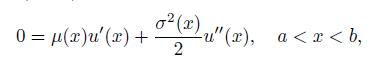
with boundary conditions u

(a) = 0 and u

(b) = 1.

Transcribed Image Text:

= u(x) P{T