Exercise 15.7 (Cameron–Martin Formula) For a standard Brownian motion {z(t)}, suppose that E

[

exp{−

∫ t 0 q(s)z2(s)ds}

]

exists, where q(t) is a deterministic function of time t. Show that

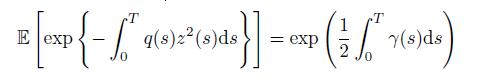
where γ(t) is a unique solution of the Riccati equation

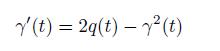
with the boundary condition γ(T) = 0. Hint: Consider d{γ(t)z2(t)} and use the result that E[Y (T)] = 1 in (14.37) for β(t) = γ(t)z(t).

Transcribed Image Text:

T E 1(s)22 (s)ds = exp { - " 9(8): (8) da}] = exp (= " \(s)ds) 2