Hahn Engineering (Example 14.5) would like to increase its return, but the project manager knows that this
Question:
Hahn Engineering (Example 14.5) would like to increase its return, but the project manager knows that this will require more cash and/or personnel. Conduct a what-if analysis of the optimal solution as the cash limitation varies from $150,000 to $270,000 in increments of $20,000, and the personnel limitation varies from 12 to 18. Summarize the returns for these solutions in the form of a heat map. Identify the solutions that represent the lowest amount of resources required to achieve each distinct return value. Write a short memo to the project manager explaining the best options and trade-offs that must be made to increase the returns.
Data from Example 14.5
Hahn Engineering’s research and development group has identified five potential new engineering and development projects; however, the firm is constrained by its available budget and human resources. Each project is expected to generate a return (given by the net present value [NPV]) but requires a fixed amount of cash and personnel. Because the resources are limited, all projects cannot be selected. Projects cannot be partially completed; thus, either the project must be undertaken completely or not at all. The data are given in Table 14.1. If a project is selected, it generates the full value of the expected return and requires the full amount of cash and personnel shown in Table 14.1. For example, if we select projects 1 and 3, the total return is $180,000 + $150,000 = $330,000, and these projects require cash totaling $55,000 + $24,000 = $79,000 and 5 + 2 = 7 personnel.
To model this situation, we define the decision variables to be binary, corresponding to either not selecting or selecting each project, respectively. Define xi = 1 if project i is selected and 0 if it is not selected. By multiplying these binary variables by the expected returns, the objective function is
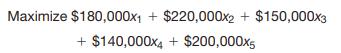
Because cash and personnel are limited, we have the following constraints
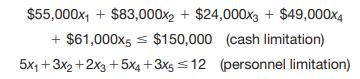
Note that if projects 1 and 3 are selected, then x1 = 1 and x3 = 1, and the objective and constraint functions equal
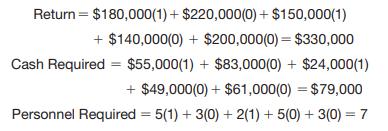
Step by Step Answer:






