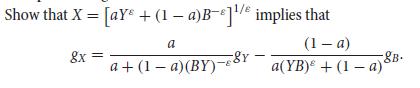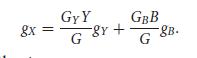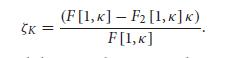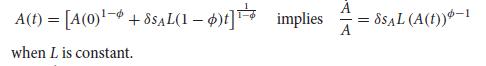Introduction To Economic Growth 3rd Edition Charles I. Jones, Dietrich Vollrath - Solutions

Dive into the world of economics with "Introduction To Economic Growth, 3rd Edition" by Charles I. Jones and Dietrich Vollrath. Enhance your learning experience with our comprehensive resources, featuring online solutions and answers key to every question. Explore our solution manual and solutions PDF, offering step-by-step answers to solved problems. Whether you're in search of a test bank or chapter solutions, our instructor manual guides you through each concept. This textbook is your go-to resource, offering free downloads of questions and answers, ensuring you have all the tools needed to excel in your economic studies.

9.2 Consumption growth In the general model, show that c∗ increases when a increases. To do this, solve (9.2) for x = (c/a)1/α and use this to eliminate x from (9.1).Then use the first-order condition for utility maximization to analyze the relationship between c and a.
9.1 Generalized basic model Assume that the relation between consumption and pollution is described by the more general function c = af (x), where f (x) > 0 and f (x) < 0. The objective function can then be written as U(x) = u(af (x)) − v(x).1. State the necessary condition for utility
8.2 CES pollution growth rate Show that X = [aY + (1 - a) B-] 1/ implies that gx = a (1 - a) gB a+(1-a)(BY)-8Y a(YB)+(1-a)
8.1 Pollution growth rate Show that X(t) = G(Y(t), B(t)) implies that Gy Y gx = GBB GY+ gB. G
7.3 Abatement share Derive equation (7.17).
7.2 z Dynamics Show that the dynamics of z is globally stable in the model of Section 7.4.
7.1 Scale, Technology, and Composition effects Derive equation (7.2).
6.2 Land and energy Suppose that both land and labor are inputs in the production function, that is(1) Show that the model is stable, by deriving and analyzing a differential equation for z in this case.(2) What is the long-run growth rate of y in this case? Y=KTBE (AL)-a-B-v
6.1 CES income shares Derive the income shares in Section 6.3.
5.3 Increasing returns to scale Consider a growth model with the following production function:Y = KαTβ(ALY)μ.Here we do not impose any assumptions about the magnitudes of the exponents; their sum may be smaller than, equal to, or larger than unity.As in the previous models the capital–output
5.2 CES income shares Show that the income shares in the CES case are those that are given in Section 5.4.
5.1 Income shares Show that the income shares are constant in the general case, if AL/K and BT/K are constant.
4.4 Directed technological change with a CES production function Consider the special case when the production function of this model takes the CES form Y =α(BK)ε + (1 − α)(A(1 − sA − sB)L)ε1/εand the equations in (4.12) still apply. Follow the same steps as in Section 4.4 to make it
4.3 Income share Given the production function Y(t) = F[B(t)K(t), A(t)LY(t)], show that the income share of capital is (F[1,K] F2 [1,K]K) SK F[1,K]
4.2 Growth in A 2 Show that A(t) implies A=88AL (1-4).
4.1 Growth in A 1 Show that = SSAL (A(t))-1 A A(t) = [A(0) + 8sAL(1 )] implies when L is constant. A
3.5 Convergence in y Given that ˜k ˜k∗ and f(k) -(n+g+8), show that ak ()-a < 0.
3.4 The Cobb–Douglas case In Section 3.2 we claimed that the Solow equation in the Cobb–Douglas case,˙˜k= s˜ kα − (n + g + δ)˜ k, has the solutionWhile it is a bitdifficult to show that the latter expressionis the solution for the former, it is straightforward to show that the latter
3.3 Dividing Y by K In exercise 2.3 you showed that division of the production function by K yields the functionUse this to derive a differential equation in ˜l. Analyze the dynamics of ˜l graphically. = 8 (1), where g'(I) > 0, g" (I) < 0 and 1 = (AL)/K. Using this in (3.17), we have K -(0)-8 =
3.2 CES income shares Start from the production function on intensity form, f (k) = (αkε+(1 − α))1/ε. Compute the income share of capital.
3.1 CES steady state Compute k∗ in the CES case, assuming that the steady state defined by(3.8) exists.
2.3 Dividing Y by K As mentioned in Section 2.2.3, an alternative way of transforming the production function into efficiency units is to divide the production function by K: Y || = | F [K, AL)] = F [K A]. K Now define Thus 1 Y | - 2 K and 7= AL K 1 2 -[]) Show that g'() > 0 and g"() < 0. g
2.2 Balanced growth Assume a growth path, along which ˜k is constant. Show that the growth path is balanced, that is consistent with the Kaldor facts.
2.1 CES and Inada The CES function (2.5) does not satisfy the Inada conditions. Show this.
Energy’s share in a CES production function. Consider the following production function: Y = F(K,E,L) = (Kr + (BE) r ) a>p(AL) 1-a. (a) What are the returns to scale in this production function? Answer this question by considering what happens to output if K, E, and L are doubled. (b) What are
Robustness of the growth-drag calculations. In the Nordhaus-style calculation of the growth drag, we assumed a land share of 10 percent and an energy share of 10 percent. As some of the discussion in the chapter suggested, these values may be too high. Redo the growth-drag calculation and the t
Solving for t. Show how to derive the solution for t in equation (10.10). Calculate the values for t that correspond to interest rates of 4 percent and 8 percent.
Optimal extraction rate. Suppose that the capital-output ratio is constant and that the real interest rate takes the constant value r. Using the energy model in Section 10.1, solve for the constant rate of extraction s*E that maximizes the present discounted value of output per worker. Explain and
A model with land and energy. Derive the steady-state growth rate of output per worker in a model with both land and energy. In particular, assume the production function for output is given by Y = BKa XbEg L1-a-b-g and that the inputs evolve as described in this chapter.
Transition dynamics in the natural resources model. For the Solow model with natural resources in Section 10.1, show that K>Y does indeed converge to a constant. Calculate the value of this constant. Also, show that the growth rate of the capital-output ratio, and hence the growth rate of output
The idea production function. What is the economic justifi cation for thinking that the production function for new ideas takes the form given in equation (9.6)? In particular, why might this production function exhibit increasing returns to scale?
Growth over the very long run. Historical evidence suggests that growth rates have increased over the very long run. For example, growth was slow and intermittent prior to the Industrial Revolution. Sustained growth became possible after the Industrial Revolution, with average growth rates of per
Market structure in the Lucas model. Think about the market structure that underlies the Lucas model. Do we need perfect or imperfect competition? Do we need externalities? Discuss.
Physical investments in the Lucas model. Does a permanent increase in sK have a growth effect or a level effect in the Lucas model? Why?
Population growth in the AK model. Consider the AK model in which we do not normalize the size of the labor force to one. (a) Using the production function in equation (9.5) and the standard capital accumulation equation, show that the growth rate of output depends on L.(b) What happens if L is
A changing land share. 12 In Section 8.3.3 we mentioned the role of structural transformation in contributing to sustained growth. Consider an economy that produces two goods, an agricultural good and a manufacturing good. An amount YA of the agricultural good can be produced using land and labor
Changes in basic education. Assume there is an increase in the basic skills, u, that each child receives. This may be because of the introduction of universal primary schooling, for example. In the quantity/ quality model in Section 8.4, what effect does this have on the amount of education
The importance of growth rates versus productivity levels. Consider two economies, A and B. Both economies are described by the model in Section 8.3, having a population growth function similar in form to that in Figure 8.6. You know that the population growth function’s peak is at L # >L =
The Black Death. In Section 8.2.1 we discussed how a major drop in the size of the population could actually raise living standards. Consider an economy that is described by the model in that section and is currently at the steady state level of population L*. (a) There is a one-time drop in
Discuss the meaning of the quotation that began this chapter.
Social infrastructure and the investment rate. Suppose that rates of return to capital are equalized across countries because the world is an open economy, and suppose that all countries are on their balanced growth paths. Assume the production function looks like Y = IKaL1-a, where I refl ects
Can differences in the utilization of factors of production explain differences in TFP? Consider a production function of the form Y = IKa(hL)1-a, where I denotes total factor productivity and the other notation is standard. Suppose I varies by a factor of ten across countries, and assume a = 1>3.
Cost-benefi t analysis. Suppose an investment project yields a profi t of $100 every year, starting one year after the investment takes place. Assume the interest rate for computing present values is 5 percent. (a) If F = $1,000, is the investment worth undertaking? (b) What if F = $5,000? (c) What
in Chapter 5.) (a) Construct a graph with h . >h on the vertical axis and A>h on the horizontal axis. In the graph, plot two lines: h . h = mecua A h b and h . >h = g. (Note that we’ve assumed g = 1.) What do these two lines mean, and what is the signifi cance of the point where they intersect?
Openness to technology transfer. This problem considers the effect on an economy’s technological sophistication of an increase in the openness of the economy to technology transfer. Specifi cally, it looks at the short-run and long-run effects on h of an increase in m. (Hint: look back at Figure
The role of m. Provide some economic intuition for the role played by the parameter m. What values of m guarantee that h>A is less than one?
Understanding growth rates. How does the model explain the differences in growth rates that we observe across countries?
Understanding levels of income. This model explains differences in the level of income across countries by appealing to differences in sK and u. What is unsatisfying about this explanation?
The importance of A versus h in producing human capital. How might one pick a value of g to be used in the empirical analysis of the model (as in Chapter 3)? Other things equal, use this value to discuss how differences in skills affect output per worker in the steady state, compared to the model
The share of the surplus appropriated by inventors (from Kremer 1998). In Figure 5.5, fi nd the ratio of the profi t captured by the monopolist to the total potential consumer surplus available if the good were priced at marginal cost. Assume that marginal cost is constant at c and the demand
and the discussion surrounding this fi gure in Chapter 4 that the number of scientists and engineers engaged in R&D has been growing faster than the rate of population growth in the advanced economies of the world. To take some plausible numbers, assume population growth is 1 percent and the growth
The future of economic growth (from Jones 2002). Recall from Figure
Too much of a good thing? Consider the level of per capita income along a balanced growth path given by equation (5.11). Find the value for sR that maximizes output per worker along a balanced growth path for this example. Why is it possible to do too much R&D according to this criterion?
An increase in the productivity of research. Suppose there is a onetime increase in the productivity of research, represented by an increase in u in Figure 5.1. What happens to the growth rate and the level of technology over time?
Pricing with increasing returns to scale. Consider the following production function (similar to that used earlier for ColdAway): Y = 100 * (L - F), where Y is output, L is labor input, and F is a fi xed amount of labor that is required before the fi rst unit of output can be produced (like a
Provision of goods. Explain the role of the market and the government in providing each of the goods in the previous question.
Classifying goods. Place the following goods on a chart like that in Figure 4.1—that is, classify them as rivalrous or nonrivalrous and by the extent to which they are excludable: a chicken, the trade secret for Coca-Cola, music from a compact disc, tropical rainforests, clean air, and a
The Mankiw-Romer-Weil (1992) model. As mentioned in this chapter, the extended Solow model that we have considered differs slightly from that in Mankiw, Romer, and Weil (1992). This problem asks you to solve their model. The key difference is the treatment of human capital. Mankiw, Romer, and Weil
Reconsidering the Baumol results. J. Bradford DeLong (1988), in a comment on Baumol’s convergence result for the industrialized countries over the last century, pointed out that the result could be driven by the procedure through which the countries were selected. In particular, DeLong noted two
Galton’s fallacy (based on Quah 1993). During the late 1800s, Sir Francis Galton, a famous statistician in England, studied the distribution of heights in the British population and how the distribution was evolving over time. In particular, Galton noticed that the sons of tall fathers tended
What are state variables? The basic idea of solving dynamic models that contain a differential equation is to fi rst write the model so that along a balanced growth path, some state variable is constant. In Chapter 2, we used y>A and k>A as state variables. In this chapter, we used y>Ah and k>Ah.
Policy reforms and growth. Suppose an economy, starting from an initial steady state, undertakes new policy reforms that raise its steady-state level of output per worker. For each of the following cases, calculate the proportion by which steady-state output per worker increases and, using the
0.028 0.234 Assume that g + d = .075, a = 1>3 and c = .10 for all countries. Using equation (3.9), estimate the steady-state incomes of these economies, relative to the United States. Consider two extreme cases: (a) the 1990 TFP ratios are maintained, and (b) the TFP levels converge completely. For
0.102
Cameroon
0.015
0.213
Thailand
0.014
0.144
Argentina
0.012
0.246
Canada
0.010
0.204
Where are these economies headed? Consider the following data: yˆ97 sK u n Aˆ 90 United States
Solow (1956) versus Solow (1957). In the Solow model with technological progress, consider an economy that begins in steady state with a rate of technological progress, g, of 2 percent. Suppose g rises permanently to 3 percent. Assume a = 1>3. (a) What is the growth rate of output per worker
Can we save too much? Consumption is equal to output minus investment: c = (1 - s)y. In the context of the Solow model with no technological progress, what is the savings rate that maximizes steady-state consumption per worker? What is the marginal product of capital in this steady state? Show this
Manna falls faster. Suppose that there is a permanent increase in the rate of technological progress, so that g rises to g$. Sketch a graph of the growth rate of output per worker over time. Be sure to pay close attention to the transition dynamics.
An income tax. Suppose the U.S. Congress decides to levy an income tax on both wage income and capital income. Instead of receiving wL + rK = Y, consumers receive (1 - t)wL + (1 - t)rK = (1 - t)Y. Trace the consequences of this tax for output per worker in the short and long runs, starting from
An increase in the labor force. Shocks to an economy, such as wars, famines, or the unifi cation of two economies, often generate large fl ows of workers across borders. What are the short-run and longrun effects on an economy of a one-time permanent increase in the stock of labor? Examine this
A decrease in the investment rate. Suppose the U.S. Congress enacts legislation that discourages saving and investment, such as the elimination of the investment tax credit that occurred in 1990. As a result, suppose the investment rate falls permanently from s$ to s&.Examine this policy change in

Introduction To Economic Growth 3rd Edition Charles I. Jones, Dietrich Vollrath - Solutions

Step by Step Answers