For each of following 2 × 2 matrices, find the determinant to determine whether the matrix issingular or nonsingular, and indicate the rank of the matrix.

.With |A| ≠ 0, A is nonsingular. Both rows and columns, therefore, are linearly independent. With two rows and columns linearly independent, the rank of A is 2: ρ(A) = 2.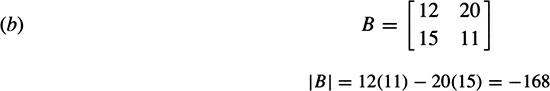

B is nonsingular; ρ(B) = 2.

With |C| = 0, C is singular. There is linear dependence between its rows and columns. Since there is, in effect, only one independent row and one independent column, ρ(C) = 1. Closer inspection reveals that row 1 is 1.5 times row 2, and column 2 is 1.25 times column 1.

The determinant does not exist because only square matrices have determinants. With only two rows, the highest possible rank of the matrix is 2: ρ(D) = 2.

Transcribed Image Text:

(a) 5 2 A = [3, 4] 94 |A| 5(4) 2(9) = 2 =