Redo Problem 7.14, using the following data: In Fig. 7-13, with the isocost line tangent to constraint
Question:
Redo Problem 7.14, using the following data: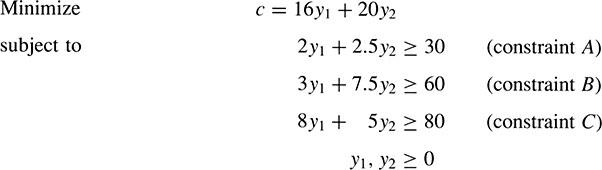
In Fig. 7-13, with the isocost line tangent to constraint A, there is no unique optimal feasible solution. Any point on the line between (5, 8) and (10, 4) will minimize the objective function subject to the constraints. Multiple optimal solutions occur whenever there is linear dependence between the objective function and one of the constraints. In this case, the objective function and constraint A both have a slope of -4/5 and are linearly dependent. Multiple optimal solutions, however, in no way contradict the extreme point theorem since the extreme points (5, 8) and (10, 4)
are also included in the optimal solutions: c = 16(5) + 20(8) = 240 and c = 16(10) +20(4) = 240.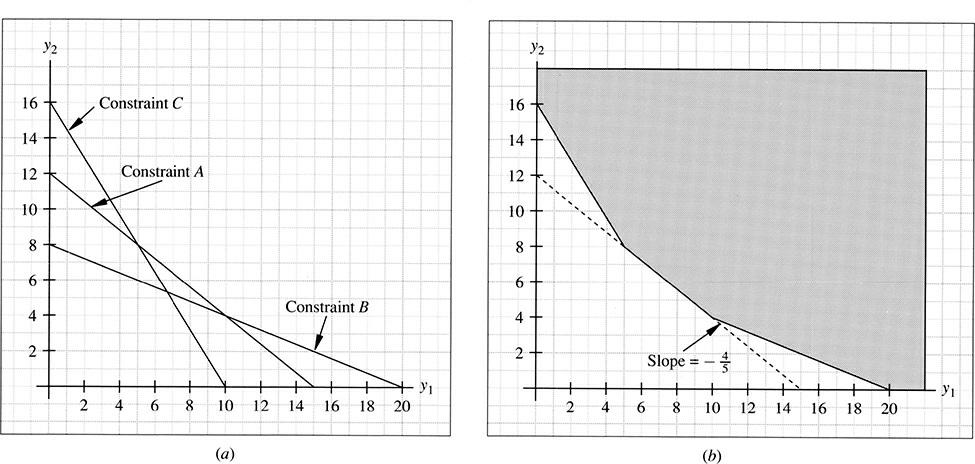
Step by Step Answer:

Schaum S Outline Of Mathematical Methods For Business Economics And Finance
ISBN: 978-1264266876
2nd Edition
Authors: Luis Moises Pena Levano





