A flexible chain of length L is suspended between two poles of equal height separated by a
Question:
A flexible chain of length L is suspended between two poles of equal height separated by a distance 2M (Figure 10). By Newton’s laws, the chain describes a curve (called a catenary) with equation y = a cosh(x/a) + C. The constant C is arbitrary and a is the number such that L = 2a sinh(M/a). The sag s is the vertical distance from the highest to the lowest point on the chain.

Let M be a fixed constant. Show that the sag is given by s = a cosh(M/a) − a.
(a) Calculate ds/da.
(b) Calculate da/dL by implicit differentiation using the relation L = 2a sinh(M/a).
(c) Use (a) and (b) and the Chain Rule to show that
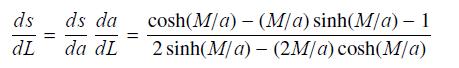
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





