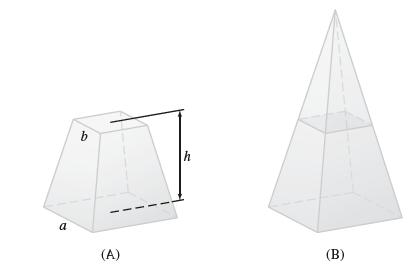
A frustum of a pyramid is a pyramid with its top cut off [Figure 22(A)]. Let V be the volume of a frustum of height h whose base is a square of side a and whose top is a square of side b with a > b ≥ 0.
(a) Show that if the frustum were continued to a full pyramid, it would have height ha/(a − b) [Figure 22(B)].
(b) Show that the cross section at height x is a square of side (1/h)(a(h − x) + bx).
(c) Show that V = 1/3 h(a² + ab + b²). A papyrus dating to the year 1850 bce indicates that Egyptian mathematicians had discovered this formula almost 4000 years ago.

Transcribed Image Text:

a b (A) h (B)