A light wave of wavelength travels from A to B by passing through an aperture (circular

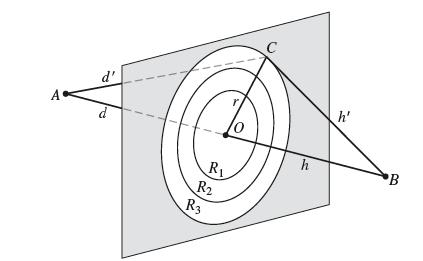
A light wave of wavelength λ travels from A to B by passing through an aperture (circular region) located in a plane that is perpendicular to AB (see Figure 11 for the notation). Let ƒ(r) = d' + h'; that is, ƒ(r) is the distance AC + CB as a function of r. 

(a) Show that ƒ(r) = √d² + r² + √h² + r², and use the Maclaurin polynomial of order 2 to show that

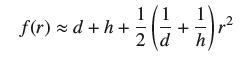
(b) The Fresnel zones, used to determine the optical disturbance at B, are the concentric bands bounded by the circles of radius R_n such that ƒ(R_n) = d + h + nλ/2. Show that R_n ≈
√nλL, where L = (d⁻¹ + h⁻¹)⁻¹.
(c) Estimate the radii R₁ and R₁₀₀ for blue light (λ = 475 × 10⁻⁷ cm) if d = h = 100 cm.

Transcribed Image Text:

² + 1² ( 1² + 1 ) ²2²2 2 f(r) ≈d+h+