A path r(t) = (x(t), y(t)) follows the gradient of a function (x, y) if the tangent
Question:
A path r(t) = (x(t), y(t)) follows the gradient of a function ƒ(x, y) if the tangent vector r'(t) points in the direction of ∇ƒ for all t. In other words, r'(t) = k(t)∇ƒr(t) for some positive function k(t). In this case, r(t) crosses each level curve of ƒ(x, y) at a right angle.
Show that if the path r(t) = (x(t), y(t)) follows the gradient of ƒ(x, y), then
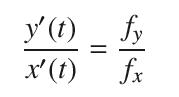
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





