\(C\) is the path from \(P\) to \(Q\) in Figure 17 that traces \(C_{1}, C_{2}\), and \(C_{3}\) in the orientation indicated, and \(\mathbf{F}\) is a vector field such that

\[
\int_{C} \mathbf{F} \cdot d \mathbf{r}=5, \quad \int_{C_{1}} \mathbf{F} \cdot d \mathbf{r}=8, \quad \int_{C_{3}} \mathbf{F} \cdot d \mathbf{r}=8
\]

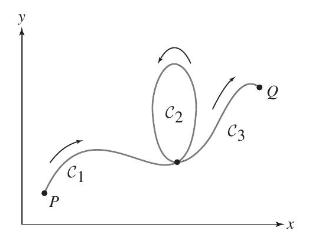
Determine:
(a) \(\int_{-C_{3}} \mathbf{F} \cdot d \mathbf{r}\)
(b) \(\int_{C_{2}} \mathbf{F} \cdot d \mathbf{r}\)
(c) \(\int_{-C_{1}-C_{3}} \mathbf{F} \cdot d \mathbf{r}\)

Transcribed Image Text:

P C1 C2 C3 X