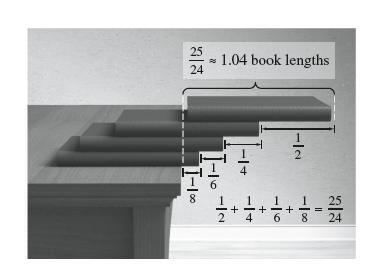
How far can a stack of identical books (of mass m and unit length) extend without tipping
Question:
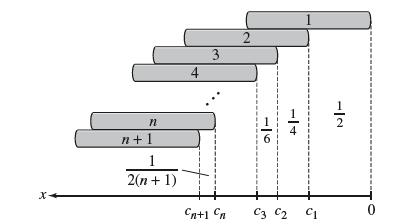
How far can a stack of identical books (of mass m and unit length) extend without tipping over? The stack will not tip over if the (n + 1)st book is placed at the bottom of the stack with its right edge located at or before the center of mass of the first n books (Figure 6). Let cn be the center of mass of the first n books, measured along the x-axis, where we take the positive x-axis to the left of the origin as in Figure 7. Recall that if an object of mass m1 has center of mass at x1 and a second object of m2 has center of mass x2, then the center of mass of the system has x-coordinate
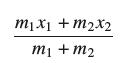

Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





