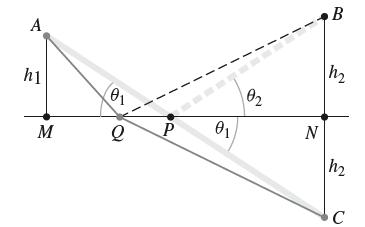
In this exercise, we use Figure 42 to prove Heron’s principle of Example 7 without calculus. By definition, C is the reflection of B across the line MN (so that BC is perpendicular to MN and BN = CN). Let P be the intersection of AC and MN. Use geometry to justify the following:

Example 7

Transcribed Image Text:

= 0₂. (a) ΔΡΝ Β and ΔΡNC are congruent and θα (b) The paths APB and APC have equal length. (c) Similarly, AQB and AQC have equal length. (d) The path APC is shorter than AQC for all Q # P. Conclude that the shortest path AQB occurs for Q = P.