Let (a) Show that there is a unique point P = (a, b) on g(x, y) =
Question:
Let ![]()
(a) Show that there is a unique point P = (a, b) on g(x, y) = 1 where ∇ƒP = λ∇gP for some scalar λ.
(b) Refer to Figure 13 to determine whether ƒ(P) is a local minimum or a local maximum of ƒ subject to the constraint.
(c) Does Figure 13 suggest that ƒ(P) is a global extremum subject to the constraint?
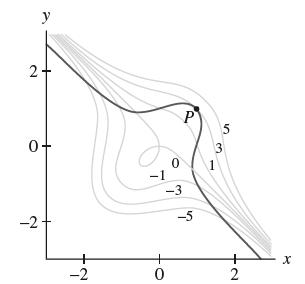
Transcribed Image Text:
f(x, y) = x + xy + y, g(x, y) = x - xy +y
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Answer rating: 100% (1 review)
a The gradients of fare Vf 3x yx tion Vf Vg is or 3y and Vg 3x 3x yx 3y 1 3x y x 3y 3x y x 3y Equati...View the full answer

Answered By

Nicholas Maina
Throughout my tutoring journey, I've amassed a wealth of hands-on experience and honed a diverse set of skills that enable me to guide students towards mastering complex subjects. My proficiency as a tutor rests on several key pillars:
1. Subject Mastery:
With a comprehensive understanding of a wide range of subjects spanning mathematics, science, humanities, and more, I can adeptly explain intricate concepts and break them down into digestible chunks. My proficiency extends to offering real-world applications, ensuring students grasp the practical relevance of their studies.
2. Individualized Guidance:
Recognizing that every student learns differently, I tailor my approach to accommodate various learning styles and paces. Through personalized interactions, I identify a student's strengths and areas for improvement, allowing me to craft targeted lessons that foster a deeper understanding of the material.
3. Problem-Solving Facilitation:
I excel in guiding students through problem-solving processes and encouraging critical thinking and analytical skills. By walking learners through step-by-step solutions and addressing their questions in a coherent manner, I empower them to approach challenges with confidence.
4. Effective Communication:
My tutoring proficiency is founded on clear and concise communication. I have the ability to convey complex ideas in an accessible manner, fostering a strong student-tutor rapport that encourages open dialogue and fruitful discussions.
5. Adaptability and Patience:
Tutoring is a dynamic process, and I have cultivated adaptability and patience to cater to evolving learning needs. I remain patient through difficulties, adjusting my teaching methods as necessary to ensure that students overcome obstacles and achieve their goals.
6. Interactive Learning:
Interactive learning lies at the heart of my approach. By engaging students in discussions, brainstorming sessions, and interactive exercises, I foster a stimulating learning environment that encourages active participation and long-term retention.
7. Continuous Improvement:
My dedication to being an effective tutor is a journey of continuous improvement. I regularly seek feedback and stay updated on educational methodologies, integrating new insights to refine my tutoring techniques and provide an even more enriching learning experience.
In essence, my hands-on experience as a tutor equips me with the tools to facilitate comprehensive understanding, critical thinking, and academic success. I am committed to helping students realize their full potential and fostering a passion for lifelong learning.
4.90+
5+ Reviews
16+ Question Solved
Related Book For 

Question Posted:
Students also viewed these Mathematics questions
-
Find the extreme values of (x, y) = x 2 + 2y 2 subject to the constraint g(x, y) = 4x 6y = 25. (a) Show that the Lagrange equations yield 2x = 42, 4y = -62. (b) Show that if x = 0 or y = 0, then the...
-
Let (, A) = ([0, 1), B(0,1)), and let the transformation T be defined by T(x) = cx, x ( [0, 1), where c is a constant in (0, 1). Then show that there is no probability measure P on B(0,1) such that...
-
Managing Scope Changes Case Study Scope changes on a project can occur regardless of how well the project is planned or executed. Scope changes can be the result of something that was omitted during...
-
Instructions for the Partnership Exercise: Your assignment is to correct a defective three person partnership agreement. You need to name at least three partners in your partnership agreement. If you...
-
Dehydration of natural gas is necessary to prevent the formation of gas hydrates, which can plug valves and other components of a gas pipeline, and also to reduce potential corrosion problems. Water...
-
Exploring Vero Beachs Financial Report Refer to the financial statements of the City of Vero Beach in Chapter 3 and to Table 81. 1. What amount did Vero Beach report in its government-wide statements...
-
What fashion companies has Nabil either worked for or had his work sold through? LO.1
-
The Kohler Chemical Manufacturing Company produces two primary chemical products to be used as base ingredients for a variety of products. The 2016 budget for the two products (in thousands) was as...
-
To estimate the Jana Inc's WACC, you have obtained the following information (1) The firm's nonsable bonds mature in 20 years have an 0% and coupon, a par le of $1,000, and a market price of $1,050....
-
Find the point (a, b) on the graph of y = ex where the value ab is the least.
-
Find the minimum and maximum values of the function subject to the given constraint. f(x, y, z) = xy + xz, x + y + z = 4
-
Use the Food Critics Club (FCC) graph database that was created and used earlier in the text for use with Neo4j. Write a query to return the shortest path based only on reviews between members...
-
The air in an automobile tire with a volume of \(0.015 \mathrm{~m}^{3}\) is at \(30^{\circ} \mathrm{C}\) and \(140 \mathrm{kPa}\) (gage). Determine the amount of air that must be added to raise the...
-
Convex Productions has just received a contract to film a commercial video that will air during a major sporting event in North America, and then be available on-demand through banner advertisements...
-
The following data (and annotations) for March 2016 are for the work in process account of the first of Olympus Companys four departments used in manufacturing its nly product. Assuming that Olympus...
-
If relative volatility can be assumed constant over the change in concentration for each fraction, Eq. \((9-13)\) can be adapted to the collection of fractions from a simple binary batch...
-
(a) Design a PI controller for Problem 8.6-4(b). (b) Design a PD controller for Problem 8.6-4(c). (c) Use the results of parts (a) and (b) to repeat Problem 8.6-4(d). Problem 8.6-4(b) (c) (d) (b)...
-
Turi's Tee Shirt Shack sold 36 shirts one day. Each short-sleeved tee shirt costs $12, and each long-sleeved tee shirt costs $18. Total receipts for the day were $522. How many of each kind of shirt...
-
If someone's Z-score for a variable was 0.67. Their score is a significant extreme score. Their score is not significant. O Their score is slightly above average. O Their score is an outlier.
-
Identify each conic without completing the square or rotating axes. 3x 2 xy + 2y 2 + 3y + 1 =
-
Identify each conic without completing the square or rotating axes. x 2 6xy + 9y 2 + 2x 3y 2 = 0
-
Given the equation 41x 2 24xy + 34y 2 25 = 0, rotate the axes so that there is no xy-term. Analyze and graph the new equation.
-
September 1 . Purchased a new truck for $ 8 3 , 0 0 0 , paying cash. September 4 . Sold the truck purchased January 9 , Year 2 , for $ 5 3 , 6 0 0 . ( Record depreciation to date for Year 3 for the...
-
Find the NPV for the following project if the firm's WACC is 8%. Make sure to include the negative in your answer if you calculate a negative. it DOES matter for NPV answers
-
What is the value of a 10-year, $1,000 par value bond with a 12% annual coupon if its required return is 11%?

Study smarter with the SolutionInn App


