Question: Let (mathbf{F}=leftlangle-x^{2} y, x, 0ightangle). Referring to Figure 19 , let (C) be the closed path (A B C D). Use Stokes' Theorem to evaluate

Let $\mathbf{F}=\left\langle-x^{2} y, x, 0ightangle$. Referring to Figure 19 , let $C$ be the closed path $A B C D$. Use Stokes' Theorem to evaluate $\int_{C} \mathbf{F} \cdot d \mathbf{r}$ in two ways. First, regard $C$ as the boundary of the rectangle with vertices $A, B, C$, and $D$. Then treat $C$ as the boundary of the wedge-shaped box with an open top.

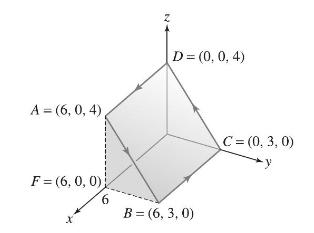
A = (6, 0, 4) F=(6, 0, 0); 6 z D=(0, 0,

A = (6, 0, 4) F=(6, 0, 0); 6 z D=(0, 0, 4) B= (6, 3,0) C=(0, 3, 0)

Step by Step Solution

★★★★★

3.49 Rating (169 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Stokes theorem connects a surface integral over a vector field to a line integral over the boundary of the surface Specifically it states that int intS abla times mathbfF cdot dmathbfS ointC mathbfF c... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Calculus 4th Questions!

A uniform magnetic field B has constant strength b in the z-direction [that is, B = (0, 0, b)]. (a) Verify that A = 12 B Ã r is a vector potential for B, where r = (x, y, 0). (b) Calculate the...

The following additional information is available for the Dr. Ivan and Irene Incisor family from Chapters 1-5. Ivan's grandfather died and left a portfolio of municipal bonds. In 2012, they pay Ivan...

Betty Brunett, an employee who is single, spent $2,000 in unreimbursed business expenses associated with her $20,000 annual salary. Included in those expenses were $1,000 of travel and $1,000 of dues...

Use Green's Theorem to evaluate the line integral. Orient the curve counterclockwise unless otherwse indicated. Let $\mathbf{F}(x, y)=\left\langle 2 x e^{y}, x+x^{2} e^{y}ightangle$ and let $C$...

Apply Stokes' Theorem to evaluate $\oint_{C} \mathbf{F} \cdot d \mathbf{r}$ by finding the flux of $\operatorname{curl}(\mathbf{F})$ across an appropriate surface. \(\mathbf{F}=\langle x z, x y,...

1. A player throws a fair die and simultaneously flips a fair coin. If the coin lands heads, then she wins twice, and if tails, then one-half of the value that appears on the die. Determine her...

Math 636 Final - Quiz Component 1. The system of linear equations 2x2 x3 = 3 2x1 + x2 + 2x3 = 1 x1 + x2 + 3x3 = 2 (a) is consistent with a unique solution. (b) is consistent with infinitely many...

Which of the following activities takes place once the mission has been established? The firm develops alternative or backup missions in case the original mission fails. Strategy and implementation...

For a reversible reaction A P kf is 4.0 10 2 s 1 and kb is half of kf . Initial concentration of A is 2.0 mol dm 3 . At what time the concentration of B will be 1.0 mol dm 3 .

Question 6 Consider the following code: struct node { int data; struct node * next; } typedef struct node NODE; NODE ? * * malloc ( sizeof ( struct NODE ) ) ; ptr struct NODE *

LO 1-1 Discuss the roles and activities of a companys human resource management function. page 6

Let R be the region bounded by y = ln x, the x-axis, and the line x = a, where a > 1. a. Find the volume V 1 (a) of the solid generated when R is revolved about the x-axis (as a function of a). b....

a. Let R be the region bounded by the graph of f(x) = x -p and the x-axis, for x 1. Let V 1 and V 2 be the volumes of the solids generated when R is revolved about the x-axis and the y-axis,...

Let R 1 be the region bounded by the graph of y = e -ax and the x-axis on the interval [0, b] where a > 0 and b > 0. Let R 2 be the region bounded by the graph of y = e -ax and the x-axis on the...

What is the tax rate of C Corporations in the US? What is the legal basis? Elaborate. Enable Ginger Cannot connect to Ginger Check your internet connection or reload the browserDisable in this text...

Which of the following function headers best fits a type conversion operator to convert an object of the Fraction class to type double, so that one can use implicit type conversions such as double...

Flounder Company is constructing a building. Construction began on February 1 and was completed on December 31. Expenditures were $1,932,000 on March 1, $1,212,000 on June 1, and $3,081,610 on...