Let \(\mathcal{D}\) be the region bounded by a simple closed curve \(C\). A function \(\varphi(x, y)\) on \(\mathcal{D}\) (whose second-order partial derivatives exist and are continuous) is called harmonic if \(\Delta \varphi=0\), where \(\Delta \varphi\) is the Laplace operator defined in Eq.(12).

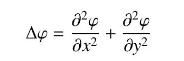
Use the results of Exercises 48 and 49 to prove the mean-value property of harmonic functions: If \(\varphi\) is harmonic, then \(I_{\varphi}(r)=\varphi(P)\) for all \(r\).

Data From Exercise 48

Let \(P=(a, b)\) and let \(C_{r}\) be the circle of radius \(r\) centered at \(P\). The average value of a continuous function \(\varphi\) on \(C_{r}\) is defined as the integral
\[
I_{\varphi}(r)=\frac{1}{2 \pi} \int_{0}^{2 \pi} \varphi(a+r \cos \theta, b+r \sin \theta) d \theta
\]
(a) Show that
\[
\frac{\partial \varphi}{\partial \mathbf{n}}(a+r \cos \theta, b+r \sin \theta)=\frac{\partial \varphi}{\partial r}(a+r \cos \theta, b+r \sin \theta)
\]
(b) Use differentiation under the integral sign to prove that
\[
\frac{d}{d r} I_{\varphi}(r)=\frac{1}{2 \pi r} \int_{C_{r}} \frac{\partial \varphi}{\partial \mathbf{n}} d s
\]
(c) Use Exercise 47 to conclude that
\[
\frac{d}{d r} I_{\varphi}(r)=\frac{1}{2 \pi r} \iint_{\mathcal{D}(r)} \Delta \varphi d A
\]
where \(\mathcal{D}(r)\) is the interior of \(C_{r}\).

Data From Exercise 47

Let \(\mathbf{n}\) be the outward-pointing unit normal vector to a simple closed curve \(C\). The normal derivative of a function \(\varphi\), denoted \(\frac{\partial \varphi}{\partial \mathbf{n}}\), is the directional derivative \(D_{\mathbf{n}}(\varphi)=abla \varphi \cdot \mathbf{n}\). Prove that
\[
\oint_{C} \frac{\partial \varphi}{\partial \mathbf{n}} d s=\iint_{\mathcal{D}} \Delta \varphi d A
\]
where \(\mathcal{D}\) is the domain enclosed by a simple closed curve \(C\). Hint: Let \(\mathbf{F}=abla \varphi\). Show that \(\frac{\partial \varphi}{\partial \mathbf{n}}=\mathbf{F}^{*} \cdot \mathbf{T}\), where \(\mathbf{T}\) is the unit tangent vector, and apply Green's Theorem.

Transcribed Image Text:

= 0x2 +