Let \(\mathcal{S}\) be the unit square in the \(x y\)-plane shown in Figure 14, oriented with the normal pointing in the positive \(z\)-direction. Estimate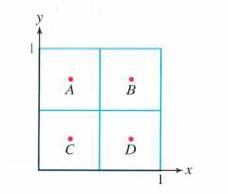
\[
\iint_{\mathcal{S}} \mathbf{F} \cdot d \mathbf{S}
\]
where \(\mathbf{F}\) is a vector field whose values at the labeled points are
\[
\begin{array}{ll}
\mathbf{F}(A)=\langle 2,6,4angle, & \mathbf{F}(B)=\langle 1,1,7angle \\
\mathbf{F}(C)=\langle 3,3,-3angle, & \mathbf{F}(D)=\langle 0,1,8angle
\end{array}
\]

Transcribed Image Text:

A C B D 1 X